PS-AMO

Azimuth moveout is a prestack partial migration operator that transforms 3D prestack data with a given offset and azimuth into equivalent data with a different offset and azimuth.

PP-AMO is not a single trace to trace transformation. It is a partial migration operator that moves events across midpoints according to their dip. Due to the nature of PS-data, where multiple coverage is obtained through common conversion point gathers (CCP), the PS-AMO operator moves events across common conversion points according to their geological dip.

Theoretically, the cascade of any imaging operator with its corresponding forward-modeling operator generates an AMO operator Biondi (2000). Our PS-AMO operator is a cascade operation of PS-DMO and inverse PS-DMO.

The 2D PS-DMO smile Harrison (1990); Rosales (2002); Xu et al. (2001) extends to 3D by replacing the offset and midpoint coordinates for the offset and midpoint vectors, respectively. The factor D, responsible for the CMP to CCP transformation, also transforms to a vector quantity. The PS-DMO smile in 3D takes the form of:

 

$$\frac{t_0^2}{t_n^2} + \frac{\Vert \vec{y} \Vert^2}{\Vert \vec{H} \Vert^2} =1,$$ (1)

where,

 

$$\Vert \vec{y}\Vert^2 = \Vert \vec{x} + \vec{D}\Vert^2,$$ (2)

$$\vec{H} = \frac{2\sqrt{\gamma}}{1+\gamma} \vec{h},$$ (3)

and

$$\vec{D}=\left[ 1 + \frac{4\gamma \Vert \vec{h}\Vert ^2}{v_p^... ...Vert \vec{h} \Vert^2} \right] \frac{1-\gamma}{1+\gamma} \vec{h}$$

Here, $\vec{x}$ is the midpoint position vector, $\vec{h}$ is the offset vector and $\gamma=\frac{v_p}{v_s}$ ratio.

The PS-AMO operator, a cascade operator of PS-DMO and inverse PS-DMO, takes the form of:

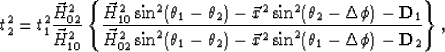$$t_2^2=t_1^2 \frac{\vec{H}_{02}^2}{\vec{H}_{10}^2}\left \{ \f... ...}^2\sin^2(\theta_1 - \Delta\phi) - \mbox{{\bf D}}_2} \right \},$$ (4)

where

$$\begin{eqnarray} \mbox{{\bf D}}_1 & = & \vec{D}_{10}^2\sin^2(\theta_1 - \theta_2... ...ta_1 - \Delta\phi)\sin(\theta_1 - \theta_2) \cos\lambda. \nonumber\end{eqnarray}$$

This operator reduces to the traditional expression of PP-AMO Biondi et al. (1998) for $\vec{D} = \vec{0}$ (i.e. $\gamma=1$).

Although the PP-AMO operator is velocity independent, this independence doesn't propagate for the PS-AMO operator. The PS-AMO operator depends on the P velocity and the $\frac{v_p}{v_s}$ ratio. We assume that the velocity of the new trace position is the same as in the previous position.