A hybrid attenuation scheme

In the multiple attenuation case, most of the problems encountered with the adaptive subtraction technique stem from the correlation that might exist between the noise and signal. In addition, the minimum energy assumption forces the residual (the signal) to be white, which is not valid all the time. Fortunately we can derive a fitting goal that can cope with interfering noise and signal and non-white spectrum.

In Guitton (2002), I presented a method that approximates covariance operators with pef. The goal was basically to obtain independent and identically distributed (iid) residual components. I propose using the same approach for the filter estimation in adaptive filtering.

Following this idea, I have the new fitting goal  

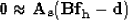$$\bf{0} \approx \bf{A_s}(\bf{Bf_h-d})$$ (4)

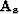where $\bf{A_s}$ is a pef that whitens the signal spectrum only. The corresponding least-squares estimate for 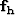$\bf{f_h}$ becomes  

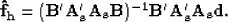$$\bf{\hat{f}_h} = (\bf{B'A_s'A_sB})^{-1}\bf{B'A_s'A_sd}.$$ (5)

If the signal has a white spectrum, then this new estimate of the filter 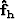$\bf{\hat{f}_h}$ is identical to the estimate in equation (3). If the signal is not white, then this new estimate is going to be more accurate than the estimate in equation (3). More specifically, the noise and signal do not have to be orthogonal any more.

I call this scheme hybrid because it puts back together two worlds: the world of adaptive subtraction and the world of pef. Nonetheless, this method is not a pattern-based technique because the multiples and primaries are not separated according to their spatial predictability. I am only proposing to unbias the filter estimation.

Once the filter has been estimated [equation (5)] I compute the noise and signal as follows:

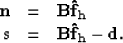$$\begin{array} {rcl} \bf{n}&=&\bf{B\hat{f}_h} \\ \bf{s}&=&\bf{B\hat{f}_h-d}. \end{array}$$ (6)

One unsolved problem is the pef estimation. I give few guidelines in the next section.