




Next: A simple 1D problem
Up: Guitton and Verschuur: adaptive
Previous: Guitton and Verschuur: adaptive
A classical approach for attenuating multiples consists of building
a multiple model Verschuur et al. (1992) and adaptively subtracting
this model from the multiple infested-data by estimating shaping filters
Dragoset (1995); Liu et al. (2000); Rickett et al. (2001).
The estimation of the shaping filters is usually done in a least-squares
sense making these filters relatively easy to compute.
In some cases, however, a least-squares criterion can lead to undesirable
artifacts. This happens when, for example, the relatively strong primaries are
surrounded by multiples, such that the filter tends to distort primary energy
as well.
In this paper we show that the estimation of shaping filters with
the 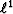 -norm gives better results than with
the
-norm gives better results than with
the 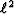 -norm when multiples and primaries have noticeable
amplitude differences. We first illustrate this with a simple 1D problem
that highlights the limits of the least-squares approach. In a second
synthetic example, we attenuate internal multiples and show that
the
-norm when multiples and primaries have noticeable
amplitude differences. We first illustrate this with a simple 1D problem
that highlights the limits of the least-squares approach. In a second
synthetic example, we attenuate internal multiples and show that
the 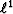 -norm gives far better results than does
-norm gives far better results than does 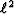 .To finish, we utilize shaping filters on a multiple contaminated
gather from a seismic survey showing that the
.To finish, we utilize shaping filters on a multiple contaminated
gather from a seismic survey showing that the 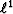 -norm
leads to a substantial attenuation of the multiples.
-norm
leads to a substantial attenuation of the multiples.





Next: A simple 1D problem
Up: Guitton and Verschuur: adaptive
Previous: Guitton and Verschuur: adaptive
Stanford Exploration Project
6/7/2002
![]() -norm gives better results than with
the
-norm gives better results than with
the ![]() -norm when multiples and primaries have noticeable
amplitude differences. We first illustrate this with a simple 1D problem
that highlights the limits of the least-squares approach. In a second
synthetic example, we attenuate internal multiples and show that
the
-norm when multiples and primaries have noticeable
amplitude differences. We first illustrate this with a simple 1D problem
that highlights the limits of the least-squares approach. In a second
synthetic example, we attenuate internal multiples and show that
the ![]() -norm gives far better results than does
-norm gives far better results than does ![]() .To finish, we utilize shaping filters on a multiple contaminated
gather from a seismic survey showing that the
.To finish, we utilize shaping filters on a multiple contaminated
gather from a seismic survey showing that the ![]() -norm
leads to a substantial attenuation of the multiples.
-norm
leads to a substantial attenuation of the multiples.