Introduction

Shot profile migration includes three different steps: downgoing wavefield propagation, upgoing wavefield backward propagation and imaging. The last step, imaging, is based on Claerbout's imaging principle Claerbout (1971). According to this principle, a reflector exists at a point where the upgoing and the downgoing wavefields coincide in time and space (Figure 1).

 

jon
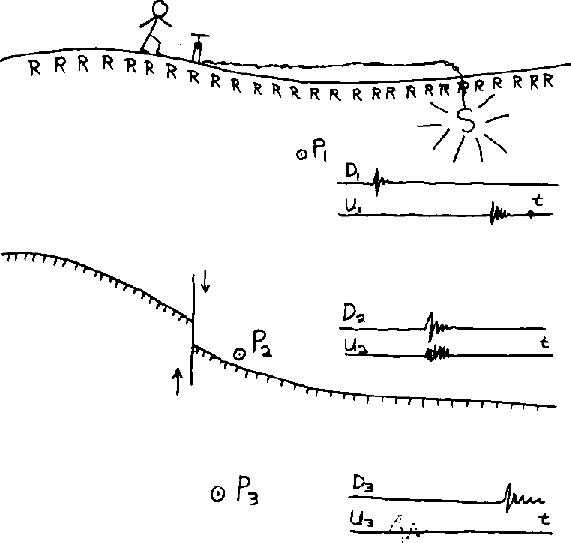
Figure 1 Reflector mapping imaging principle, note that the reflector exists at a point where the upgoing and downgoing wavefields coincide in time and space. Taken from Claerbout (1971)

There are two distinct aspects behind this principle: the kinematic (coincidence in time and space of upgoing and downgoing wavefields) and the dynamic (reflection strength at the coincidence point). Conventional migration schemes Jacobs (1982) determine the reflection strength in each subsurface point taking into account only the downgoing and the upgoing wavefields at that location. But these approaches don't consider that the reflectors in the subsurface are spatially correlated. We discuss a multidimensional imaging condition that makes the reflectivity strength dependent on the downgoing and upgoing wavefields in a neighborhood of the subsurface point.

Based on the equivalence of the deconvolution imaging condition with the exact solution of the least squares fitting goal, we propose a regularization scheme for the imaging condition that has the potential of including the previous knowledge of the image in the regularization operator. This regularization approach has been used to steer the final image in least squares inversion Prucha and Biondi (2002).

First, we explore a multidimensional deconvolution imaging condition. No clear results were obtained using this approach yet, but it allows us to study the difficulties of multidimensional deconvolution. Second, a least squares regularized scheme for the imaging condition is stated.

Finally we test, in a synthetic experiment, a space variable damping factor to improve conventional industry imaging condition. In this case we only consider point to point dependence of the reflection strength.