




Next: Image perturbation by residual
Up: Sava and Biondi: Image
Previous: Introduction
In migration by downward continuation, the wavefield at depth
 (
( ) is obtained by phase-shift from the wavefield at
depth z (
) is obtained by phase-shift from the wavefield at
depth z ( )
)
|  |
(1) |
where the depth wavenumber 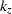 depends linearly
through a Taylor series expansion
on its value in the reference medium (
depends linearly
through a Taylor series expansion
on its value in the reference medium ( ) and
the slowness in the depth interval from z to
) and
the slowness in the depth interval from z to  ,
,
 and
and  :
:
|  |
(2) |
where, by definition,  .
.
If we denote the wavefield downward continued through the
reference velocity as 
|  |
(3) |
we obtain
|  |
(4) |
The Born approximation linearizes the phase-shift exponential
 , such that we can write
, such that we can write
|  |
(5) |
Therefore, at any particular depth level,
the wavefield perturbation  is
is
|  |
(6) |
which we can also write as
|  |
(7) |
The image perturbation is simply obtained from the wavefield
perturbation by summation over frequencies:
|  |
(8) |





Next: Image perturbation by residual
Up: Sava and Biondi: Image
Previous: Introduction
Stanford Exploration Project
9/18/2001
![]() (
(![]() ) is obtained by phase-shift from the wavefield at
depth z (
) is obtained by phase-shift from the wavefield at
depth z (![]() )
)
![]()
![]() , such that we can write
, such that we can write
