Next: Cost-cutting avenues
Up: Vlad and Biondi: Log-stretch
Previous: Stretching and aliasing
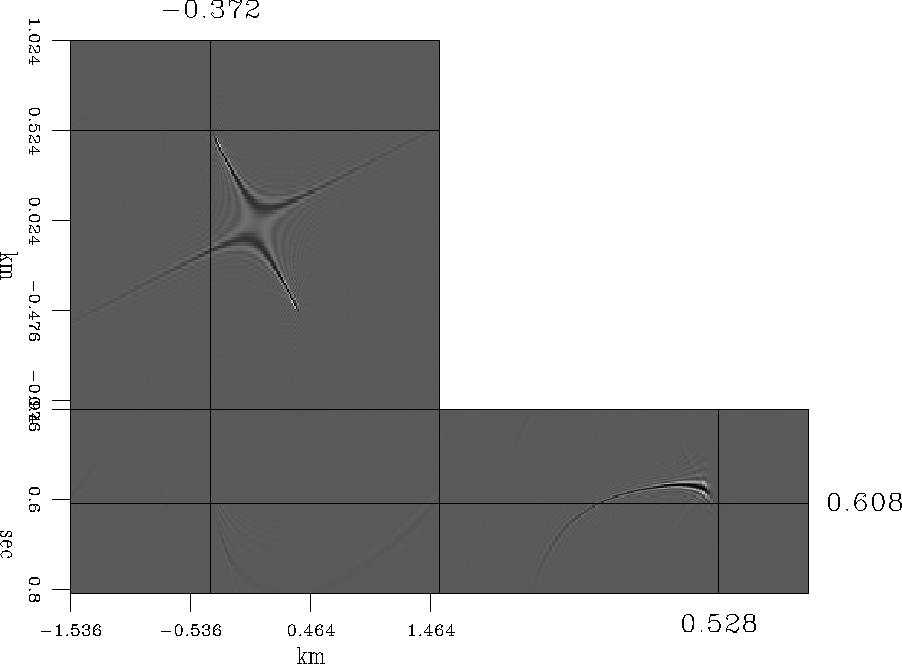
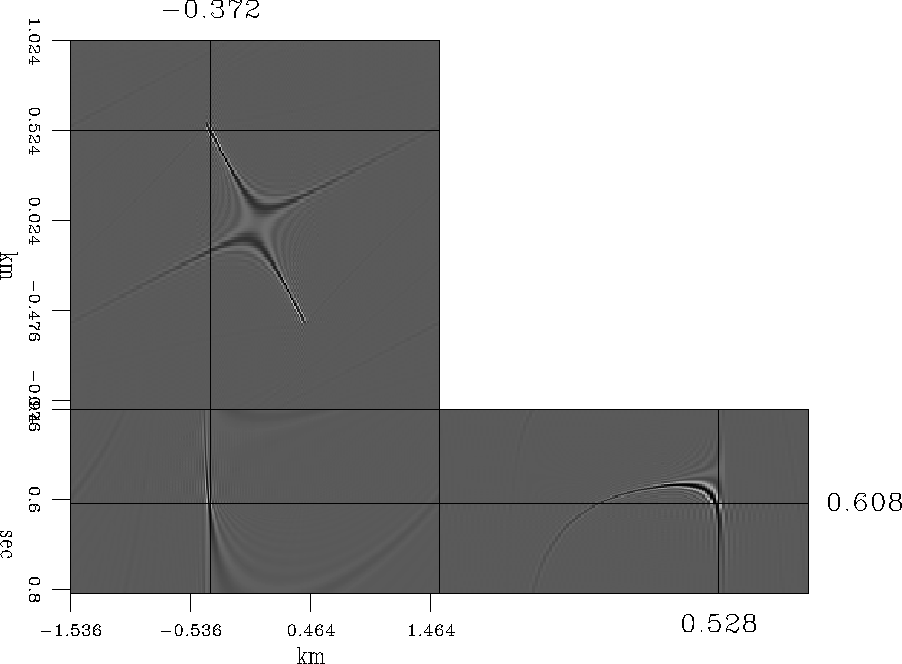
As it can be seen in Fig. 3, the impulse response of
the AMO computed in the log-stretch, frequency-wavenumber domain has
some artifacts: high amplitude, large saddle corners. Low temporal
frequencies and high spatial slopes are also present. These artifacts can be eliminated easily
using a f-k filter, which is described below.
impresp2
Figure 3 AMO impulse response artifacts





Suppose we want to attenuate all spatial frequencies k that are larger than a certain threshold 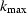 , where
, where
| 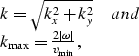 |
(10) |
with 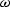 , kx and ky being the coordinates in the frequency-wavenumber domain (without logstretch), and v being the minimum apparent velocity of the events that we want the filtered data cube to contain. Thus, the data cube will become:
, kx and ky being the coordinates in the frequency-wavenumber domain (without logstretch), and v being the minimum apparent velocity of the events that we want the filtered data cube to contain. Thus, the data cube will become:
| 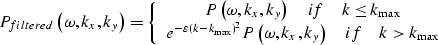 |
(11) |
Too small an  will result in an abrupt transition in the f-k domain, and thus ringing artifacts in the t-x domain. An
will result in an abrupt transition in the f-k domain, and thus ringing artifacts in the t-x domain. An  which is too big will result in no visible filtering of the targeted artifacts. Moreover,
which is too big will result in no visible filtering of the targeted artifacts. Moreover,  depends on the choice of units and the number of samples for the mx and my axes: since the exponential needs to be dimensionless, we have
depends on the choice of units and the number of samples for the mx and my axes: since the exponential needs to be dimensionless, we have
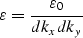
where
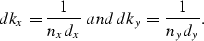
Thus, the final expression of  is
is
| 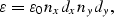 |
(12) |
where 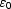 is a value that is hand-picked only once, and embedded in the code. This way, we will not have to change anything at all in the code or in the parameters in order to set
is a value that is hand-picked only once, and embedded in the code. This way, we will not have to change anything at all in the code or in the parameters in order to set 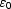 , no matter what the units of the data cube may be.
, no matter what the units of the data cube may be.
The result of the filtering can be seen in Fig. 4:
the slices through the cube are taken at exactly the same locations as
those in Fig. 3, but now the artefacts are gone.
fkfilter
Figure 4 AMO impulse response after f-k filtering










Next: Cost-cutting avenues
Up: Vlad and Biondi: Log-stretch
Previous: Stretching and aliasing
Stanford Exploration Project
9/18/2001

![]() , where
, where
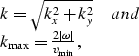
![]()
![]()