Next: Stretching and aliasing
Up: Vlad and Biondi: Log-stretch
Previous: The Azimuth Moveout
Starting from the parametric DMO relations of Black et al. (1993),
Zhou et al. (1996) derives an expression for a DMO applicable on 2D NMO-ed
data. In order to extend the expression to 3D, we only have to replace
the product kh between the wavenumber and half offset with the dot
product of the same quantities, which are vectors in the case of 3D
data. In order to perform AMO from the offset 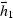 to the offset
to the offset
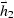 , we need to cascade one forward DMO from offset
, we need to cascade one forward DMO from offset 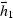 to
zero offset with a reverse DMO from zero offset to offset
to
zero offset with a reverse DMO from zero offset to offset 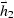 . Thus, applying log-stretch, frequency-wavenumber AMO on a 3D
cube of data
. Thus, applying log-stretch, frequency-wavenumber AMO on a 3D
cube of data 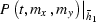 in order to obtain
in order to obtain 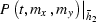 involves the following sequence of operations:
involves the following sequence of operations:
- 1.
- Apply log-stretch along the time axis on the
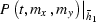 cube, with the formula:
cube, with the formula:
| 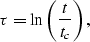 |
(1) |
where tc is the minimum cutoff time introduced to avoid taking the logarithm of zero. All samples from times smaller than tc are simply left untouched, the rest of the procedure will be applied to the cube 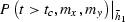 .
. - 2.
- 3D forward FFT of the
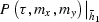 cube. The 3D forward Fourier Transform is defined as follows:
cube. The 3D forward Fourier Transform is defined as follows:
| 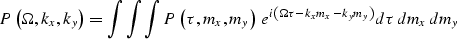 |
(2) |
It can be seen that the sign of the transform along the  -axis is opposite to that over the midpoint axes.
-axis is opposite to that over the midpoint axes.
- 3.
- For each element of the cube, perform the AMO shift:
| 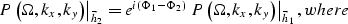 |
(3) |
| ![\begin{displaymath}
\Phi _j = \left\{ {\begin{array}
{*{20}c}
{0,\quad for\;\v...
...ight]} \right\}\quad otherwise} \\ \end{array}\;} \right.,\quad\end{displaymath}](img11.gif) |
(4) |
| 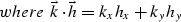 |
(5) |
and j can take the values 1 or 2.
The frequency domain variables must have incorporated in their value a 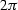 constant (they are defined according to equation (2))
constant (they are defined according to equation (2))
- 4.
- Do reverse 3D FFT in order to obtain the
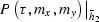 cube.
cube.
- 5.
- Do reverse log stretch along the time axis and affix to the top of the cube the slices from times smaller than tc. The final result is a
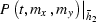 cube.
cube.
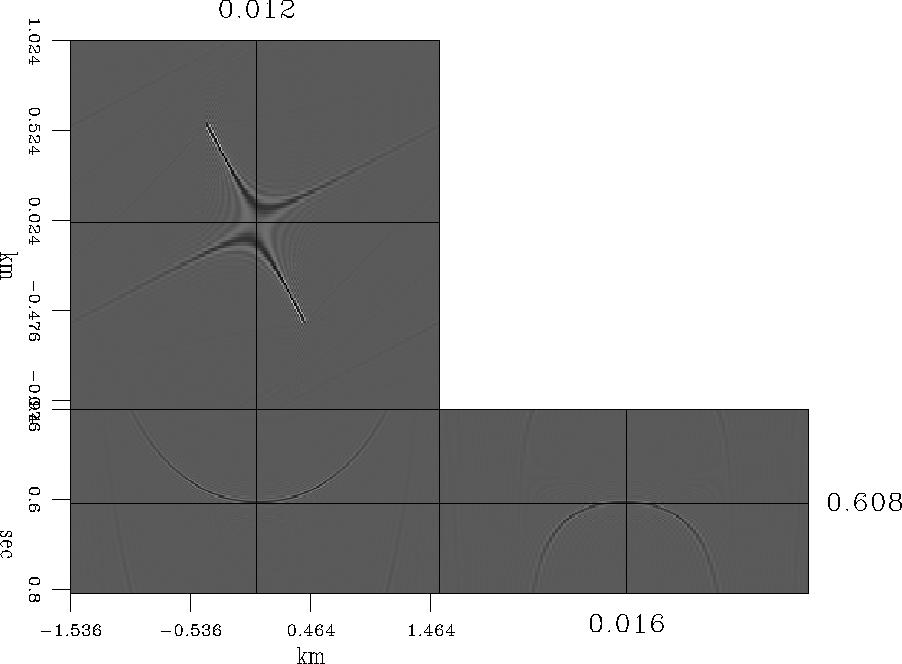
Figure 1 shows the impulse response of the above
described AMO.
impresp1
Figure 1 AMO impulse response










Next: Stretching and aliasing
Up: Vlad and Biondi: Log-stretch
Previous: The Azimuth Moveout
Stanford Exploration Project
9/18/2001
![\begin{displaymath}
\Phi _j = \left\{ {\begin{array}
{*{20}c}
{0,\quad for\;\v...
...ight]} \right\}\quad otherwise} \\ \end{array}\;} \right.,\quad\end{displaymath}](img11.gif)
![\begin{displaymath}
\Phi _j = \left\{ {\begin{array}
{*{20}c}
{0,\quad for\;\v...
...ight]} \right\}\quad otherwise} \\ \end{array}\;} \right.,\quad\end{displaymath}](img11.gif)