 |
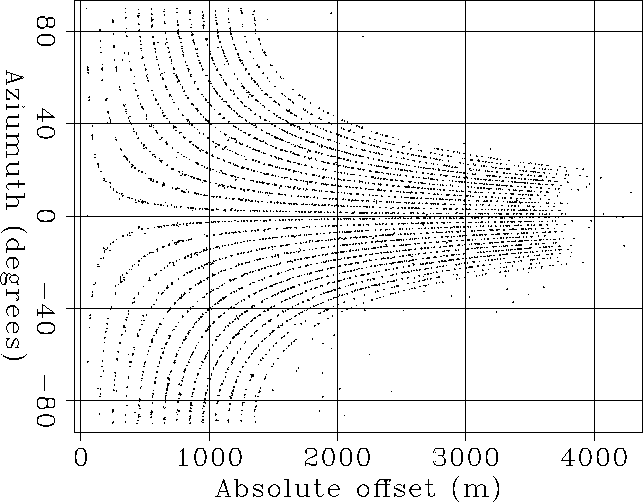
Figure 1 Offset-azimuth distribution of the land data set from South America.
We tested the geometry regularization methods presented in the previous section on a land data set recorded in South America. The data were shot with a cross-swath geometry. The shot lines are not perfectly aligned along the perpendicular to the receiver lines, but they are oriented at an angle (about 18 degrees). Figure 1 shows the plot of the absolute offset vs. azimuth for a random sample of traces in the data set. For land data, the data set has fairly narrow-azimuth acquisition geometry.
Figure 2 shows three sections (depth slice on the top, cross-line section in the middle, and in-line section on the right) of the near-angle stack of the migrated data. At a depth of about 3.2 km there is a producing reservoir with numerous wells that could be used in future work to evaluate the imaging results. The only a structural feature in the data is a steep folding/faulting at the reservoir level. There are subtle stratigraphic features at a shallower depth, such as the channel visible in the upper-left corner of the depth slice in the figure (depth of 1.9 km).
The processing sequence comprised of the following steps: a) NMO, b) geometry regularization, c) inverse NMO, d) 3-D prestack common-azimuth wave-equation migration, with the imaging step designed to preserve relative amplitudes, as discussed by Sava and Biondi 2001. The velocity model was fairly simple. The NMO velocity was slightly varying in the lateral direction. However, we migrated the data using an interval velocity only as a function of depth.
 |
 |
To test the relative performances of the different geometry
regularization methods we migrated the data after regularizing
the geometries with three different methods:
a) normalization by partial stack fold
[equation (5)];
we will simply call this method normalization.
b) normalization of the regularized and preconditioned solution
without AMO
[equation (17)];
we will simply call this method regularization,
c) normalization of the regularized and preconditioned solution
with AMO
[equation (17) with ![]() ,as in equation (19)];
we will call this method AMO regularization.
,as in equation (19)];
we will call this method AMO regularization.
The geometry regularizations produced common offset/azimuth cubes at zero azimuth and with offset sampling of 195 m, in-line midpoint sampling of 25 m, and cross-line midpoint sampling of 50 m. By assuming reciprocity, the offset sign was ignored to increase the effective fold of the common offset/azimuth cubes. Our first tests to regularize the data geometry produced common offset-azimuth cubes at zero azimuth (i.e. the data azimuth was ignored) because of the fairly limited azimuthal range at far offsets. However, we have indications that taking into account the data azimuth for the far-offset traces may be beneficial.
The offset axis was resampled at 65 m by simple interpolation before migration, to avoid offset aliasing in the downward continuation. This offset sampling was selected to avoid aliasing artifacts at the reservoir level. Finer sampling would be necessary to migrate shallower events without aliasing the higher frequencies present in the seismic signal. The effects of irregular geometries are more evident at shallow depth, and interesting stratigraphic features are visible in the migrated stack as shallow as 1 km depth. Therefore, future tests may be directed to produce high-quality images shallower than the tests that we present in this paper.