




Next: Approximation of by application
Up: Normalized partial stacking and
Previous: Normalized partial stacking and
We now analyze the properties of the approximate inverse
that is defined by the substitution of 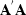 with a diagonal matrix
with a diagonal matrix 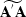 ,when the diagonal elements of
,when the diagonal elements of 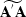 are
equal to the sum of the corresponding rows of
are
equal to the sum of the corresponding rows of 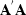 .Notice that
.Notice that 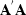 is symmetric, and thus
summing over the columns would be equivalent
to summing over the rows.
is symmetric, and thus
summing over the columns would be equivalent
to summing over the rows.
It can be noticed that the diagonal elements of
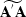 are equal
to the sum of the columns of the original operator
are equal
to the sum of the columns of the original operator 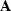 as defined in equation (1);
i.e.,
they are equal to the fold computed for each corresponding model trace.
as defined in equation (1);
i.e.,
they are equal to the fold computed for each corresponding model trace.
The weights alj are interpolator weights,
and they fulfill the constraint
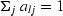 expressed in
equation (1).
It immediately follows that
expressed in
equation (1).
It immediately follows that
| 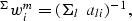 |
(10) |
which is equivalent to equation (6).
In summary, we just derived,
for the model-space inverse,
an approximation
that is easy to compute, and it is equal
to the fold normalization that
was defined by heuristic considerations.
However, the definition of the approximate inverse
can be applied when more complex imaging operators are
involved,
and for which
we do not have a simple heuristic to define the weights
that improve the results obtained by application of the adjoint operator.





Next: Approximation of by application
Up: Normalized partial stacking and
Previous: Normalized partial stacking and
Stanford Exploration Project
9/18/2001
![]() are equal
to the sum of the columns of the original operator
are equal
to the sum of the columns of the original operator ![]() as defined in equation (1);
i.e.,
they are equal to the fold computed for each corresponding model trace.
as defined in equation (1);
i.e.,
they are equal to the fold computed for each corresponding model trace.
![]() expressed in
equation (1).
It immediately follows that
expressed in
equation (1).
It immediately follows that