




Next: Data dependent parameterization
Up: Focusing operator inversion
Previous: Forward Modeling
Optimization is done by calculating the updates of the model parameters by means of the difference between the traveltimes of the modeled and the observed focusing operators.
The relation between the traveltime data and the model parameters is assumed to be linear:
| 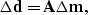 |
(1) |
where 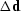 contains the difference in traveltimes,
contains the difference in traveltimes, 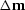 contains the update in model parameters, and
contains the update in model parameters, and 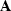 describes the linear relation between these traveltimes and the model parameters.
It might be very difficult to solve for the model vector
describes the linear relation between these traveltimes and the model parameters.
It might be very difficult to solve for the model vector 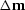 in terms of the data vector
in terms of the data vector 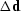 , as matrix
, as matrix 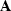 generally is not invertible. However, the generalized matrix inverses can be obtained by several methods. The generalized inverse obtained by these methods is defined by a dagger:
generally is not invertible. However, the generalized matrix inverses can be obtained by several methods. The generalized inverse obtained by these methods is defined by a dagger:
| 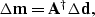 |
(2) |
When a least squares method is chosen to obtain a generalized inverse, an update of 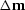 is calculated by:
is calculated by:
| 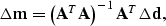 |
(3) |
where 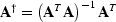 is the generalized inverse. Another way to obtain the generalized inverse is for example by singular value decomposition (SVD). Berryman (2001a) gives a profound overview of the available methods and their capacities. Several methods of approximating the generalized inverse will be presented in one of the next sections.
is the generalized inverse. Another way to obtain the generalized inverse is for example by singular value decomposition (SVD). Berryman (2001a) gives a profound overview of the available methods and their capacities. Several methods of approximating the generalized inverse will be presented in one of the next sections.





Next: Data dependent parameterization
Up: Focusing operator inversion
Previous: Forward Modeling
Stanford Exploration Project
9/18/2001