![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to deal with non-stationarity.
The simplest approach Yilmaz (1987) is to apply multiple stationary
filters and interpolate the results. This approach, however, gives
incorrect spectral response in the interpolated areas Pann and Shin (1976).
) to deal with non-stationarity.
The simplest approach Yilmaz (1987) is to apply multiple stationary
filters and interpolate the results. This approach, however, gives
incorrect spectral response in the interpolated areas Pann and Shin (1976).
Following Claerbout (1998a) and Margrave (1998), I extend the
concept of a filter to that of a filter-bank, which
is a set of N filters: one filter for every point in the
input/output space.
I identify ![]() with the filter corresponding to the
with the filter corresponding to the
![]() location in the input/output vector, and the coefficient,
ai,j, with the
location in the input/output vector, and the coefficient,
ai,j, with the ![]() coefficient of the filter,
coefficient of the filter,
![]() .
.
Margrave (1998) describes two closely related alternatives which
both reduce to normal convolution in the limit of stationarity.
The first approach is to place the filters in the columns of the
matrix, ![]() . This associates a single filter with a single
point in the output space, and defines non-stationary
convolution:
. This associates a single filter with a single
point in the output space, and defines non-stationary
convolution:
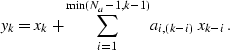 |
(116) |
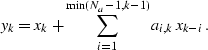 |
(117) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to an
impulse at the
) to an
impulse at the ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to an
impulse at the
) to an
impulse at the
As an illustration, consider the differences between matrices,
![]() and
and ![]() below, which
represent, respectively, non-stationary convolution and
combination with a causal three-point (Nf=3) filter-bank,
below, which
represent, respectively, non-stationary convolution and
combination with a causal three-point (Nf=3) filter-bank,
![]() , to vectors of length, N=5. The two are equivalent in the
stationary limit; however, while the columns of
, to vectors of length, N=5. The two are equivalent in the
stationary limit; however, while the columns of
![]() contain filters,
contain filters, ![]() , the columns of
, the columns of
![]() do not.
do not.
![\begin{displaymath}
{\bf F}_{\rm conv} =
\left[ \begin{array}
{ccccccc}
1 & 0 & ...
...1 & 0 \\ 0 & 0 & 0 & f_{25} & f_{15} & 1 \\ \end{array} \right]\end{displaymath}](img285.gif)