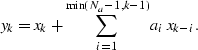
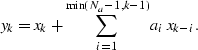 |
(112) |
The adjoint operator, ![]() , which describes time-reversed
filtering with filter
, which describes time-reversed
filtering with filter ![]() , can similarly be expressed by
considering the rows of the matrix-vector equation,
, can similarly be expressed by
considering the rows of the matrix-vector equation,
![]() , as follows,
, as follows,
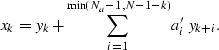 |
(113) |
The helicon Fortran90 module Claerbout (1998a) exactly implements the
linear operator (and adjoint) pair described by
equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) explicitly prescribes internal boundary
conditions near k=0; however, since
) explicitly prescribes internal boundary
conditions near k=0; however, since ![]() is causal, no
particular care is needed near k=N-1. On the other hand,
equation (
is causal, no
particular care is needed near k=N-1. On the other hand,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) explicitly imposes internal boundary
conditions near k=N-1, and no care is needed near k=0.
It is possible to rewrite equations (
) explicitly imposes internal boundary
conditions near k=N-1, and no care is needed near k=0.
It is possible to rewrite equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and (
)
and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in a more symmetric form; however, as written,
the equations lead naturally to recursive inverses for operators,
) in a more symmetric form; however, as written,
the equations lead naturally to recursive inverses for operators,
![]() and
and ![]() .
.
Rearranging equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we obtain
), we obtain
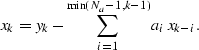 |
(114) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes the exact, analytic inverse of
causal filtering with equation (
) describes the exact, analytic inverse of
causal filtering with equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
In principle, given a filter,
).
In principle, given a filter, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can recover the original by causal
filtering with equation (
), we can recover the original by causal
filtering with equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) subject to the stability of
the inverse filtering process.
) subject to the stability of
the inverse filtering process.
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) appears very similar to polynomial
division. However, the output of polynomial division is an infinite
series, while equation (
) appears very similar to polynomial
division. However, the output of polynomial division is an infinite
series, while equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is defined only in the
range,
) is defined only in the
range, ![]() . As such, equation (
. As such, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
describes polynomial division followed by truncation.
)
describes polynomial division followed by truncation.
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can also be rewritten as
) can also be rewritten as
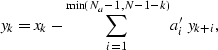 |
(115) |