




Next: Data-space weighting functions
Up: Model-space weighting functions
Previous: Numerical comparison
As it stands, the cost of computing a weighting function of this kind
is twice the cost of a single migration. Add the cost of the
migration itself, and this approach is 25% cheaper than running two
iterations of conjugate gradients, which costs two migrations per
iteration.
However, the bandwidth of the weighting functions is much lower than
that of the migrated images. This allows considerable
computational savings, as modeling and remigrating a narrow frequency
band around the central frequency produces similar weighting functions
to the full bandwidth. Repeating the first experiment
(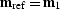 ) with half the frequencies gives a
) with half the frequencies gives a
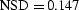 - the same as before within the noise-level of the
experiment.
- the same as before within the noise-level of the
experiment.





Next: Data-space weighting functions
Up: Model-space weighting functions
Previous: Numerical comparison
Stanford Exploration Project
5/27/2001
![]() ) with half the frequencies gives a
) with half the frequencies gives a
![]() - the same as before within the noise-level of the
experiment.
- the same as before within the noise-level of the
experiment.