




Next: Preconditioning and spectral factorization
Up: Model versus data normalization
Previous: Model versus data normalization
The generic geophysical inverse problem
Claerbout (1998a); Tarantola (1987) can be summarized as follows - given a linear
forward modeling operator 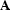 , and some recorded data
, and some recorded data 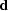 ,estimate a model
,estimate a model 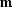 such that
such that 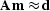 .
If the system is over-determined, the model that minimizes the
expected (L2) error in predicted data is given by the solution to
the normal equations (
.
If the system is over-determined, the model that minimizes the
expected (L2) error in predicted data is given by the solution to
the normal equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
| 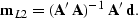 |
(92) |
Typically the matrices involved in industrial-scale geophysical
inverse problems are too large to invert directly, and we depend on
iterative gradient-based linear solvers to estimate solutions.
However, operators such as prestack depth migration are so expensive
to apply that we can only afford to iterate a handful of times, at
best.
To attempt to speed convergence, we can always change model-space
variables from 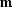 to
to  through a linear operator
through a linear operator
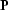 , and solve the following new system for
, and solve the following new system for  ,
,
| 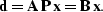 |
(93) |
When we find a solution, we can then recover the model estimate,
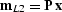 .
.
If we choose the operator 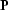 such that
such that 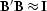 , then even simply applying the adjoint (
, then even simply applying the adjoint (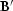 )will yield a good model estimate; furthermore, gradient-based solvers
should converge to a solution of the new system rapidly in only a few
iterations.
)will yield a good model estimate; furthermore, gradient-based solvers
should converge to a solution of the new system rapidly in only a few
iterations.





Next: Preconditioning and spectral factorization
Up: Model versus data normalization
Previous: Model versus data normalization
Stanford Exploration Project
5/27/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
![]() to
to ![]() through a linear operator
through a linear operator
![]() , and solve the following new system for
, and solve the following new system for ![]() ,
,
![]() such that
such that ![]() , then even simply applying the adjoint (
, then even simply applying the adjoint (![]() )will yield a good model estimate; furthermore, gradient-based solvers
should converge to a solution of the new system rapidly in only a few
iterations.
)will yield a good model estimate; furthermore, gradient-based solvers
should converge to a solution of the new system rapidly in only a few
iterations.