![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the impulse responses of the
45
compares the impulse responses of the
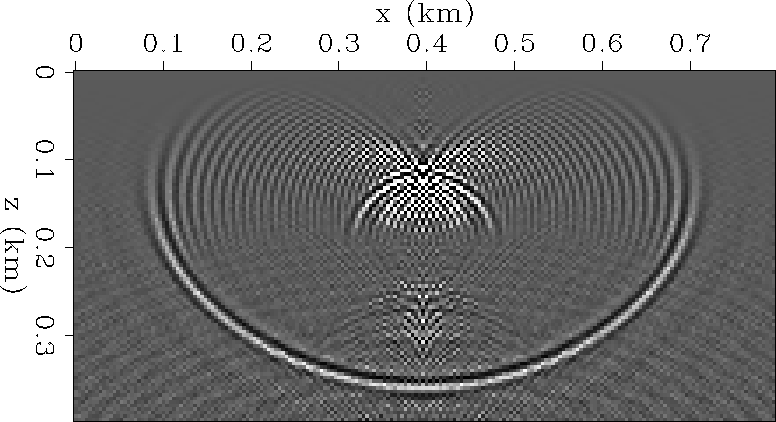
45![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a slice through the broad-band
impulse response of the 45
shows a slice through the broad-band
impulse response of the 45![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
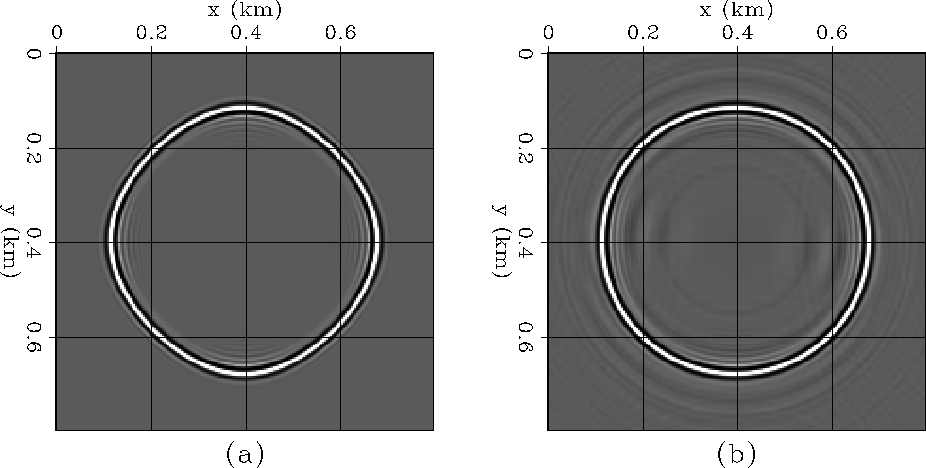
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the impulse responses of the
45
compares the impulse responses of the
45![]() equation obtained with the x-y splitting approximation
[panel (a)] and the helical factorization methodology described in
this chapter [panel (b)].
Implicit migration with the full Laplacian, instead of a splitting
approximation, produces an impulse response that is azimuthally
isotropic without the need for any phase corrections.
equation obtained with the x-y splitting approximation
[panel (a)] and the helical factorization methodology described in
this chapter [panel (b)].
Implicit migration with the full Laplacian, instead of a splitting
approximation, produces an impulse response that is azimuthally
isotropic without the need for any phase corrections.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the effects of the different boundary
conditions on the two spatial axes. The fast spatial axis (top and
bottom of Figure) have helical boundary conditions, and show
wrap-around. The slow spatial axis (left and right of Figure) has
a zero-value boundary condition, and hence is reflective.
shows the effects of the different boundary
conditions on the two spatial axes. The fast spatial axis (top and
bottom of Figure) have helical boundary conditions, and show
wrap-around. The slow spatial axis (left and right of Figure) has
a zero-value boundary condition, and hence is reflective.
For the examples in this chapter, we set the `one-sixth'
parameter Claerbout (1985), ![]() , and used the isotropic
nine-point Laplacian from equation (
, and used the isotropic
nine-point Laplacian from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) that corresponds
to
) that corresponds
to ![]() in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
 |
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
|
3Dboundary
Figure 3 Depth-slice of offset impulse response corresponding to a dip of 45 | 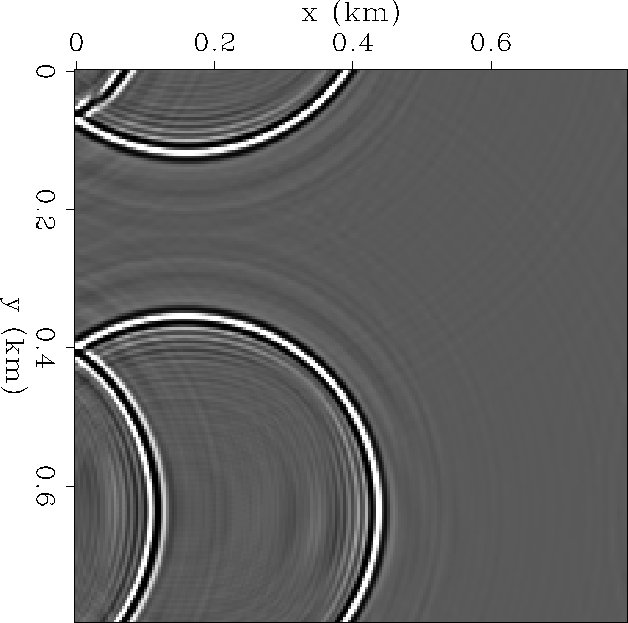 |