




Next: The Helmholtz equation
Up: Helical factorization of the
Previous: Introduction
As a simple illustration of how helical boundary conditions can lead
to recursive solutions to partial differential equations, consider
Poisson's equation, which in the constant coefficient case relates
potential, u, to source density, f, through the Laplacian
operator:
| 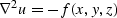 |
(13) |
Poisson's equation crops up in many different branches of physics: for
example, in electrostatics, gravity, fluid dynamics (where the fluids
are incompressible and irrotational), and steady-state temperature
studies. It also serves as a simple analogue to the wave-propagation
equations which provide the main interest of this thesis.
To solve Poisson's equation with constant coefficients on a regular
grid Claerbout (1997), we can approximate the
differential operator, 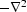 , by a convolution with a small
finite-difference filter, d.
Taking the operator,
, by a convolution with a small
finite-difference filter, d.
Taking the operator, 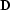 , to represent convolution with filter,
d, Poisson's equation becomes
, to represent convolution with filter,
d, Poisson's equation becomes
| 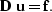 |
(14) |
Although 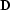 itself is a multi-dimensional convolution operator
that is not easily invertible, helical boundary
conditions Claerbout (1997) allow us to reduce the
dimensionality of the convolution to an equivalent one-dimensional
filter, which we can factor into the product of a lower-triangular
matrix,
itself is a multi-dimensional convolution operator
that is not easily invertible, helical boundary
conditions Claerbout (1997) allow us to reduce the
dimensionality of the convolution to an equivalent one-dimensional
filter, which we can factor into the product of a lower-triangular
matrix, 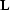 , and its transpose,
, and its transpose, 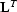 . These triangular
matrices represent causal and anti-causal convolution with a
minimum-phase filter, in the form
. These triangular
matrices represent causal and anti-causal convolution with a
minimum-phase filter, in the form
| 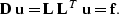 |
(15) |
The operator, 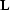 , is the helical derivative, discussed in
more detail by Claerbout (1998a).
We can calculate u directly from equation (
, is the helical derivative, discussed in
more detail by Claerbout (1998a).
We can calculate u directly from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
since
)
since 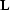 and its transpose are easily invertible by recursive
polynomial division:
and its transpose are easily invertible by recursive
polynomial division:
| 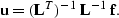 |
(16) |
The right panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the solution of the
Poisson's equation with the single source and sink shown in the left
panel. The center panel shows the intermediate result,
shows the solution of the
Poisson's equation with the single source and sink shown in the left
panel. The center panel shows the intermediate result,
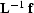 .
lapfac
.
lapfac
Figure 1
Deconvolution by a filter whose autocorrelation
is the two-dimensional Laplacian operator.
This amounts to solving the Poisson equation.
After Claerbout (1997).










Next: The Helmholtz equation
Up: Helical factorization of the
Previous: Introduction
Stanford Exploration Project
5/27/2001
![]() , by a convolution with a small
finite-difference filter, d.
Taking the operator,
, by a convolution with a small
finite-difference filter, d.
Taking the operator, ![]() , to represent convolution with filter,
d, Poisson's equation becomes
, to represent convolution with filter,
d, Poisson's equation becomes
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
since
)
since ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the solution of the
Poisson's equation with the single source and sink shown in the left
panel. The center panel shows the intermediate result,
shows the solution of the
Poisson's equation with the single source and sink shown in the left
panel. The center panel shows the intermediate result,
