




Next: ADCIG methods
Up: Applications of amplitude-preserved migration
Previous: True-amplitude migration
The ``true-amplitude'' migration defined in Equation (12)
is a good approximation in the case of mild velocity variations,
commonly labeled as ``time-migration'' problems.
In complex overburden, the so called ``depth-migration'' situations,
the reflectors are sparsely and unevenly illuminated
Rickett (2001),
therefore the amplitude corrections described in the preceding sections
may become a poor approximation.
In these cases, the amplitude term (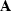 ) is neither diagonal
nor invertible because of reflections becoming evanescent and/or
moving out of the acquisition aperture.
Direct inversions are not likely to produce good results, therefore
we have to solve the inversion problem using iterative schemes
Prucha et al. (2001).
Thus, instead of simply applying ``true-amplitude'' migration,
we iteratively solve the least-squares problem described
by the optimization goal
) is neither diagonal
nor invertible because of reflections becoming evanescent and/or
moving out of the acquisition aperture.
Direct inversions are not likely to produce good results, therefore
we have to solve the inversion problem using iterative schemes
Prucha et al. (2001).
Thus, instead of simply applying ``true-amplitude'' migration,
we iteratively solve the least-squares problem described
by the optimization goal
| 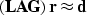 |
(14) |
where the operator 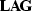 fits the reflectivity
model (
fits the reflectivity
model ( ) to the recorded data (
) to the recorded data (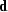 ).
).
In order to achieve fast convergence, the modeling operator has to be
as close to unitary as possible. Following the discussion in the preceding
sections, we can define the pseudo-unitary operator as
| 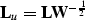 |
(15) |
for which it is immediate to verify that 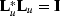 .
.
With this new operator, our least-squares problem may be rewritten as:
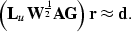
We can redefine the model variable as a new, preconditioned variable
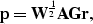
which changes the optimization problem to the simple equation:
| 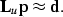 |
(16) |





Next: ADCIG methods
Up: Applications of amplitude-preserved migration
Previous: True-amplitude migration
Stanford Exploration Project
4/30/2001
![]()
![]()