HOW IT WORKS

Since I first started (with some dense algebra in Geophysics), I figured out a way to explain the basic idea with almost no math. Almost none, but a little bit will help. Since we are going ahead with almost no math, you'll need to be satisfied with getting only the vertically incident seismogram at zero-offset, but you will get all the multiple reflections of all orders with correct amplitudes too.

Let us start off with a triangle function, say the sampled function (3,2,1) which looks like a triangle when you plot it. Suppose we have a downgoing wave which is a triangle function. We like to write it as D = 3 + 2Z +Z². You can think of Z as the the ``unit delay operator'' meaning that the ``2'' comes a moment after the ``3'' and the ``1'' comes two moments later corresponding to Z². Some of you will recognize Z as the Z-transform variable but that isn't necessary here.

One of the very most interesting things you can do with a signal is take its autocorrelation or compute its energy as a function of frequency. We do this for the triangle with this expression $\overline{D} D = (3+2/Z+1/Z^2)(3+2Z+Z^2)$.If you multiply it out and look at the term that has no Z you see it is 3²+2²+1 which is the total energy. Coefficients of other powers of Z are the autocorrelation at other lags. If you remember Fourier series, you will recall that when $Z=e^{i\omega \Delta t}$ we have the Fourier transform and spectrum. The expression $\overline{D} D = (3+2/Z+1/Z^2)(3+2Z+Z^2)$represents both the autocorrelation and the spectrum of the downgoing triangle wave. It represents the autocorrelation when you look at the coefficients of the product, and it represents the spectrum when you consider numerical values for Z.

From all of this Z business, the main thing we need to recognize is that D = 3 + 2Z +Z² is a causal function meaning that the ``3'' occurs at time t=0 and everything else happens later. Likewise $\overline{D} = 3 + 2/Z +1/Z^2$ is an anticausal function meaning that the action is before t=0.

OK, now with all that theoretical background out of the way, let us put it to some use. Examine Figure 1.

 

eqcor
Figure 3 Pancake earth with prospector's boundary conditions (left) and earthquake boundary conditions (right)

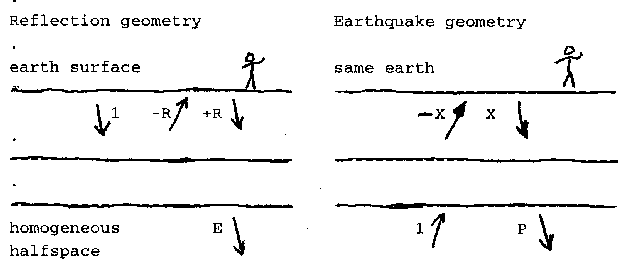It depicts a pancake earth with two different experiments. On the left is the one we are familiar with, reflection seismology. Theoretically, the geophysicist on the surface generates a downgoing impulse, the ``1''. The earth surface is called a free surface which means that it is perfectly reflecting. Any upcoming wave $U= u_1 Z + u_2 Z^2 + u_3 Z^3 + \cdots$at the earth surface will create a downgoing wave D of opposite polarity D=-U. Of course the downgoing wave hits subsurface reflectors and makes another upcoming wave ad infinitum, and it all gets very complicated with lots and lots of multiple reflections. When all is said and done, however, at the earth's surface, the upcoming wave is opposite the downgoing wave U=-D at all times except the very first. At that first moment (actually the zeroth moment) there is a downgoing wave with no upcoming wave.

The story is different for the earthquake picture. Here the impulse ``1'' comes from the opposite side of the earth. The up- and down-going waves have exactly the opposite polarity at the earth surface at all times, so we write U=-X and D=X.

Now we have finished with all our definitions and we are ready to see the most amazing correspondence between the prospectors' world and the earthquake world, and this correspondence is what gives us the potential to make big bucks in the instrumented oil field by knowing what is going on at all times.

We need the concept of conservation of energy flux. For this we need to make another simplifying assumption. You will recognize that this one isn't quite true, but it turns out to be a good engineering approximation. We assume that the earth does not absorb any acoustic energy.

We define the net downgoing energy flux as the downgoing energy minus the upgoing energy. If you are willing to think of numerical values for Z (Fourier transform) the net energy flux is actually a function of frequency. Let D(Z) represent the downgoing wave and U(Z) represent the upcoming wave. The net downgoing energy flux is $\overline{D} D - \overline{U} U$.By our assumption that no energy is absorbed, and since energy isn't piling up at any layer boundary, the downward energy flux in any one layer must equal to that in the next layer. Applying this idea to all the layers, we find that the net downgoing energy flux in the top layer matches that in the bottom halfspace. In other words, what goes in must come out, so the downgoing net energy flux anywhere is simply that at the bottom $\overline{E} E$.Thus

$$\overline{D} D - \overline{U} U = \overline{E} E$$

Next we apply this energy flux concept.

In the prospectors' world, at the earth's surface the downgoing wave is 1+R and the upcoming wave is -R. We insert these values into the net energy flux and then simplify the algebra a little.

$$\begin{eqnarray} \nonumber \overline{(1 + R)} (1 + R) \ - \ \overline{ R} R &=&\overline{E}E \\ \overline{R} \ +\ 1 \ +\ R &=&\overline{E}E \nonumber\end{eqnarray}$$

OK, the hard part is done. We are done with the math and now we only need to understand what it means. The righthand side is a spectrum or an autocorrelation. Something like $\overline{E} E = (3+2/Z+1/Z^2)(3+2Z+Z^2)$.The lefthand side has two parts, a causal waveform like $R= r_0 + r_1 Z + r_2 Z^2 + r_3 Z^3 + \cdots$and an anticausal waveform like $\overline{R}= r_0 + r_1/Z + r_2/Z^2 + r_3/Z^3 + \cdots$.This is just about it, the Big Apple. Our energy flux statement says if we compute the autocorrelation $\overline{E} E$of the escaping wave E we can look at one side of the autocorrelation to see the reflected wave R. That's amazing! We have finished with the central part of the story which is its hardest part. We are almost ready to pull it all together.

One more little step is required to get us all the way to acoustic daylight imaging. There is no more math, but there is a conceptual step, and it is a big one. (You didn't expect this to be child's play, did you?) You may have heard of the Principle of Reciprocity. Reciprocity says a common midpoint gather is symmetric about zero offset. It says if you interchange a shot with a geophone you get the same seismogram. We all know a common midpoint gather is not exactly symmetric or people would never record split spread. Nobody does record marine data with split spread. Land data is different. Only with vibrators is it practical to come close to fulfilling the requirements of reciprocity since for reciprocity to apply, both the sender and receiver should be at the same depth. Let's stop all this quibbling about practicalities of reciprocity and accept it so that we can move forward to the acoustic daylight imaging concept.

Both the earthquake person listening to natural noises and the prospector are on the same earth. One experiment says we have an impulse of excitation at the surface, and a wave E goes off to the interior of the earth. The other experiment says we have an impulse incident from the deep interior of the earth and we see the wave X on the surface. Reciprocity says that E=X.

Putting E=X into the energy flux equation gives us the main conclusion,

$$\overline{R} \ +\ 1 \ +\ R =\overline{X}X$$

which is the mathematics that says,

``One side of the autocorrelation of the earthquake seismogram is the reflection seismogram.''