When the cracks are taken to be dry, so that Ki = Gi = 0 in
(DEMK) and (DEMG), it turns out that an elegant
decoupling of the DEM equations is possible
[also see Zimmerman (1985) and Hashin (1988)]. If we consider the parameter
ratio ![]() , we find that it satisfies the
equation
, we find that it satisfies the
equation
(1-y)d (G^*/K^*)dy = -
3(1-y)(1+^*)(1-2^*) d ^*dy = P^*i - Q^*i.
Furthermore, it is generally true for dry inclusions
(not just for penny-shaped cracks)
that both P*i and Q*i are functions only of the same
ratio G*/K*, or equivalently of Poisson's ratio ![]() .Thus, we can solve (DEMratio) for either
.Thus, we can solve (DEMratio) for either ![]() or
the ratio of moduli, without considering any other equation.
or
the ratio of moduli, without considering any other equation.
It is also important to notice that the dimensionless polarization
factors P and Q
are both often close to unity, and furthermore that it is possible
that,
for special values of Poisson's ratio, we might find
P*i = Q*i. If this happens for some critical value
![]() , then the equation (DEMratio)
guarantees that this value of
Poisson's ratio will be preserved for all values of porosity, since
the right hand side vanishes initially, and therefore always.
Such a critical value is usually called a fixed point of the
equations,
and such fixed points can be either stable or unstable.
If they are unstable,
then a small deviation from the critical point causes a rapid
divergence of Poisson's ratio from the fixed point.
If they are stable, then a small deviation produces a situation in which
the value of Poisson's ratio gradually (asymptotically)
approaches the critical value. When this happens, we say the fixed
point is an attractor. For the DEM equation (DEMratio),
a fixed point that is an attractor will only be reached in the
limit
, then the equation (DEMratio)
guarantees that this value of
Poisson's ratio will be preserved for all values of porosity, since
the right hand side vanishes initially, and therefore always.
Such a critical value is usually called a fixed point of the
equations,
and such fixed points can be either stable or unstable.
If they are unstable,
then a small deviation from the critical point causes a rapid
divergence of Poisson's ratio from the fixed point.
If they are stable, then a small deviation produces a situation in which
the value of Poisson's ratio gradually (asymptotically)
approaches the critical value. When this happens, we say the fixed
point is an attractor. For the DEM equation (DEMratio),
a fixed point that is an attractor will only be reached in the
limit ![]() , but the value of Poisson's ratio will change
fairly rapidly in the direction of the attractor when the first cracks
are added to the system. Such behavior of Poisson's ratio has
been noted before by Zimmerman (1994) and by Dunn and Ledbetter (1995),
among others.
, but the value of Poisson's ratio will change
fairly rapidly in the direction of the attractor when the first cracks
are added to the system. Such behavior of Poisson's ratio has
been noted before by Zimmerman (1994) and by Dunn and Ledbetter (1995),
among others.
For penny-shaped cracks, we have
P^*i - Q^*i = 4(1-^*2)3(1-2^*) - 15 [1 + 8(1-^*)(5-^*)3(2-^*)], which has a fixed point approximately (using one step of a Newton-Raphson iteration scheme) at
_c = 236+5.
This shows that, when ![]() is very small, Poisson's ratio
for the dry cracked material tends toward small positive values.
For somewhat larger
values of
is very small, Poisson's ratio
for the dry cracked material tends toward small positive values.
For somewhat larger
values of ![]() , Poisson's ratio approaches a value proportional
to
, Poisson's ratio approaches a value proportional
to ![]() and on the order of
and on the order of ![]() .
.
For comparison, consider spherical void inclusions [see Berryman (1980) for the general expressions for P and Q]. Then, we have
P^*i - Q^*i = 1+^*2(1-2^*) - 2(4-5^*)7-5^*, which has a fixed point at
_c = 15. This result has been remarked upon previously by Zimmerman (1994). Similarly considering needle-shaped void inclusions, we have
P^*i - Q^*i = 2(1+^*)3(1-2^*) - 15 [73 + 2(3-4^*)], which has a fixed point at
_c = 18[7 - 29] 0.20185. Dunn and Ledbetter (1995) have shown that all the prolate spheroids have critical Poisson's ratios close to that for spheres. We see that needles, being the extreme case of prolate spheroids, is in agreement with this result.
Dunn and Ledbetter (1995) have shown that disk-shaped inclusions
(which are achieved by taking oblate spheroids to the
![]() limit) have a critical Poisson's ratio of
limit) have a critical Poisson's ratio of ![]() .This result and the others obtained above
are collected for comparison in TABLE 1.
.This result and the others obtained above
are collected for comparison in TABLE 1.
![\begin{displaymath}
0.15in]
\begin{tabular}
{\vert c\vert c\vert}\hline
Shape & ...
...er{36 + 2.245\pi\alpha}}$\
Disk & $0$\space \hline\end{tabular}\end{displaymath}](img72.gif)
![\begin{displaymath}
0.15in]
\begin{tabular}
{\vert c\vert c\vert}\hline
Mineral ...
...2$
Feldspar & $0.32$\space -- $0.35$\space \hline\end{tabular}\end{displaymath}](img73.gif)
To clarify the behavior of the solution of (DEMratio), we
will
do an approximate analysis by expanding the right hand side around
![]() and also note that for small
and also note that for small ![]() ,
, ![]() .Then, (DEMratio) becomes
.Then, (DEMratio) becomes
(1-y)d ^*dy 115 - 6^*5, which can easily be integrated to yield
(18 - ^*)
(18 - _m)(1-)^1h
where ![]() is the starting, or in our case the mineral, value of
Poisson's ratio, and
is the starting, or in our case the mineral, value of
Poisson's ratio, and
h = 5/6.
A more precise, and therefore more tedious, analysis of the right hand
side of (PQpenny)
gives the improved approximation (fixedpenny) for the asymptotic
value of ![]() .
.
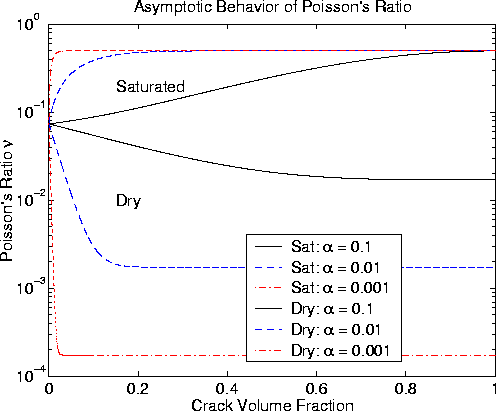 |
In Figure 8, we show the actual results for Poisson's ratio
from the full DEM in the same three examples shown in Figures 1-6.
The starting value of Poisson's ratio is ![]() .For comparison,
TABLE 2 contains a listing of various Poisson's ratios for
minerals that could be important in rocks in order to show the range
of behavior observed in nature. Except for different starting locations, we
expect the qualitative behavior of the curves for Poisson's ratio to
closely follow that of Figure 8 and (approxnu) in all cases.
.For comparison,
TABLE 2 contains a listing of various Poisson's ratios for
minerals that could be important in rocks in order to show the range
of behavior observed in nature. Except for different starting locations, we
expect the qualitative behavior of the curves for Poisson's ratio to
closely follow that of Figure 8 and (approxnu) in all cases.
[Technical note concerning the dry case: For ![]() , the Runge-Kutta
scheme used to solve the coupled DEM equations for K* and G*
was sufficiently accurate that
, the Runge-Kutta
scheme used to solve the coupled DEM equations for K* and G*
was sufficiently accurate that ![]() could be computed from these values.
However, for
could be computed from these values.
However, for ![]() and 0.001, the accuracy obtained was not
sufficient, so we instead used the same Runge-Kutta scheme but applied
it directly to (DEMratio). This approach gave very stable results.]
and 0.001, the accuracy obtained was not
sufficient, so we instead used the same Runge-Kutta scheme but applied
it directly to (DEMratio). This approach gave very stable results.]
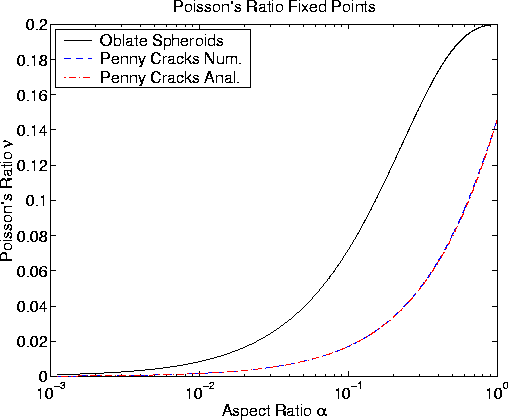 |
Figure 9 compares the results for oblate spheroids to those of
penny-shaped cracks; both curves are obtained by finding the zeros
of P-Q numerically. To provide additional insight, the curve
![]() [which was obtained by using the functional form of (fixedpenny) and
fitting the coefficient in the denominator at
[which was obtained by using the functional form of (fixedpenny) and
fitting the coefficient in the denominator at ![]() ] is also shown.
We see that the results for penny-shaped cracks deviate substantially from
those of oblate spheroids as
] is also shown.
We see that the results for penny-shaped cracks deviate substantially from
those of oblate spheroids as ![]() , but they are in agreement
at lower values of
, but they are in agreement
at lower values of ![]() . The deviations from the
results for oblate spheroids, again, are not physical and
should simply be viewed as artifacts introduced by the very low aspect ratio
limiting procedure used to obtain the approximate
formulas for penny-shaped cracks.
. The deviations from the
results for oblate spheroids, again, are not physical and
should simply be viewed as artifacts introduced by the very low aspect ratio
limiting procedure used to obtain the approximate
formulas for penny-shaped cracks.