Stabilizing the denominator

To avoid division by zero, Claerbout and Nichols (1994) suggest multiplying both the numerator and denominator in equation (4) by 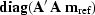${\rm\bf diag} ({\bf A}'\, {\bf A} \; {\bf m}_{\rm ref})$, and stabilizing the division by adding a small positive number to the denominator:

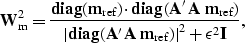$${\bf W}_{\rm m}^{2} = \frac{ {\rm\bf diag} ( {\bf m}_{\rm re... ...A} \; {\bf m}_{\rm ref}) \right\vert^2 + \epsilon^2 {\bf I}},$$ (5)

Although this does solve the problem of division by zero, the numerator and denominator will still oscillate rapidly in amplitude with the phase of the image.

Illumination, however, should be independent of the wavefield's phase. Therefore, I calculate weighting functions from the ratio of the smoothed analytic signal envelopes (denoted by <>) of the model-space images:  

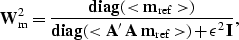$${\bf W}_{\rm m}^{2} = \frac{ {\rm\bf diag} ( <{\bf m}_{\rm r... ...A}'\, {\bf A} \; {\bf m}_{\rm ref}\gt) + \epsilon^2 {\bf I}},$$ (6)

where $\epsilon$ is a damping parameter that is related to the signal-to-noise level.