Shot to midpoint transformations

Implicit in the multi-offset imaging scheme outlined above is a transformation from shot-receiver to midpoint-offset space. Although this transformation is buried within the migration process, the subtleties associated with the conversion remain.

If the wavefields are sampled with spacing $\Delta x$, then equation (1) will image with half-offset spacing $\Delta h=\Delta x$, as shown in Figure 2 (a). Sampling in offset can be refined further by considering Figure 2 (b); however, to do so requires imaging onto midpoints which do not lie on the propagation grid.

 

cmpboth Figure 2 Imaging offsets (a) with 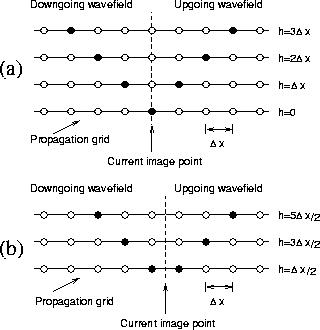$\Delta h=\Delta x$ based on equation (1) alone, and (b) with $\Delta h=\Delta x/2$, where the midpoint lies between propagation grid nodes.

This problem is experienced whenever data are transformed from shot-geophone to midpoint-offset space, and no perfect solution exists. A typical workaround is to refine the midpoint grid, and fill empty bins with zeros; however, this doubles the data-volume and hence also doubles the cost of migration. Another alternative is to process even and odd offset separately; the disadvantage of this approach is that each half of the dataset may be undersampled.

By working in the shot-geophone domain, these problems are avoided until after the migration is complete. Migration decreases the data-volume, increases the signal-to-noise ratio, and resolves locally conflicting dips. Therefore, it is easier to resample the data on whatever grid suits the interpreter after migration.