 |
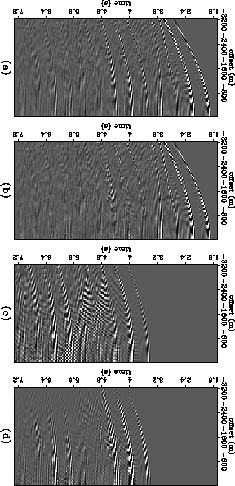
Figure 1 CMP gather with cmp_x=7000 m: (a) input gather, (b) gather after surface-multiple attenuation, (c) modeled muliples, and (d) multiples that were removed.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
Although the modeling algorithm is not the focus of this paper, we modeled surface-related multiples with a very fast 1-D algorithm. The multiple model was simply the multi-dimensional autoconvolution of common midpoint (CMP) gathers Kelamis and Verschuur (2000). This auto-convolution reduces to a multiplication in the f-k domain, and so it can be performed rapidly with multi-dimensional FFT's. More accurate multiple modelling algorithms will better attenuate multiples associated with the dipping salt-flanks. However, in 3-D examples, multiple prediction will always be imperfect, so we were interested in how this algorithm would adapt under less than ideal conditions.
Figures 1 and 2 show common-midpoint and common-offset sections before and after multiple suppression. With an imperfect multiple model, there is always a trade-off between suppressing multiples and preserving primary energy. For these results, we took a conservative approach - although some multiple energy remains in the data, hopefully all the primary energy remains too. In the areas with no salt present (e.g. cmp_x>10000 m), the multiples are almost entirely eliminated. However, in areas below the salt, especially where steeply-dipping diffracted multiples are present, some muliple energy remains.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)