Numerical Examples

To test the methodology we created a realistic synthetic example. The model consists of four reflectors, dipping at angles of $15^{\circ}$, $0^{\circ}$, $-30^{\circ}$, $-45^{\circ}$,embedded in simple linear v(z) velocities.

The velocity gradients were chosen in order to simulate a typical near seafloor velocity profile: the P-velocity model consists of an initial velocity of 1700 m/s and a gradient of 0.15 s^-1. On the other hand, the S-velocity model has an initial velocity of 300 m/s and a gradient of 0.35 s^-1.

We used ray-tracing in order to generate the data set. Figure 4 shows a common shot gather located in the center of the model. It is possible to note that the polarity flip varies with respect to the travel time as a function of the reflector dip and the $\frac{v_p}{v_s}$ ratio (Figure 2).

 

csg2 Figure 4 Common shot gather, taken in the middle of model.

Figure 5 shows two angle-domain gathers after (left) and before (right) the polarity correction in the angle domain. The events in the common angle gathers are flat, this is not obvious for the $-45^{\circ}$ event in the top of Figure 5, because of the low coverage in the modeling for that event at that depth. However, it is possible to observe that this event gets flatter with the rise in the fold, bottom of Figure 5. The flatness in the gathers implies that we used the correct velocity model for the migration. Moreover, it is possible to observe in the common angle gather before the correction that the same event changes its polarity. The point for this change is the polarity flip angle ($\theta_o$) determined by equation (9). With the P and S velocity models used for the migration and the dip map estimated by plane-wave destructors, we calculate the curve superimposed on the common angle gather, this curve represents the polarity flip angle. The angle-domain gather after the correction for the polarity inversion is in the right of Figure 5. It is clear that our methodology correctly handles the polarities after migration.

 

cag2
Figure 5 Two common angle gathers. After the prestack migration without the polarity correction (left). Before the prestack migration with the polarity correction (right). The line in the gathers mark the polarity flip angle, as a function of the dip, P-velocity and S-velocity.

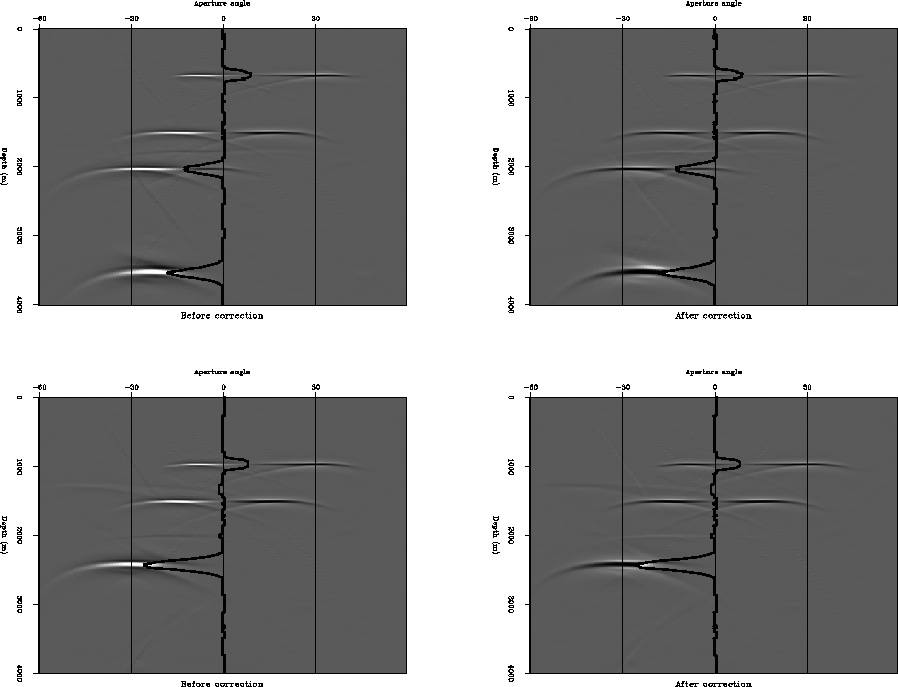Figure 6 presents the final migration results. The top represents the result with the correction in the model space (flipping in the angle domain), the center represents the result with the correction in the data space (flipping the negative offsets), and the bottom represents the migration result without any correction. It is possible to observe that the correction in the model space perfectly recovered all the events with a strong illumination; the correction in the data space produced a weaker image for the dipping events; no correction resulted in the loss of the flat event.