I run both narrow-azimuth migration methods
on the synthetic data set described above,
varying the number of crossline-offset samples
Nyh from 2 to 16.
To create data with more than one crossline offset
I padded the common-azimuth data
with zeros.
I also run a full phase-shift 3-D prestack migration
on the same data.
Full phase-shift 3-D prestack migration is equivalent
to the first method of narrow-azimuth migration,
but with the kyh range centered at kyh=0,
instead of at the 
given by equation (4).
For both the full phase-shift migration and the first narrow-azimuth methods, I kept the maximum value of the crossline offset constant at 800 m for all values of Nyh. Therefore, according to equations (6) and (5) the sampling rate of kyh was independent of Nyh, but the range of kyh decreased as Nyh decreased. Both methods lose accuracy as the range of kyh decreases, but the accuracy of full phase-shift migration degrades quicker than the accuracy of narrow-azimuth migration.
For all of these tests I used all the appropriate weighting factors, as discussed by Sava and Biondi 2001, except the phase shift and weights related to the stationary phase approximation. I excluded the stationary phase correction because as the range of kyh increases it is not anymore necessary. Indeed, the phase of the migrated images changes as the Nyh increases. However, the amplitude of the deeper reflectors decreases as Nyh increases because of the increasing amount of zero padding.
Figure 10 shows the the results of full phase-shift migration of the synthetic data set with Nyh=16. It shows the same subset of the migrated cube as in Figure 4. The front face of the cube is an inline section through the stack. The other two faces are sections through the prestack image. The kinematics of the migration are correct. The events are flat in the ADCIG shown in Figure 11. I use this results as benchmark for the narrow-azimuth and the full phase-shift migration as Nyh decreases.
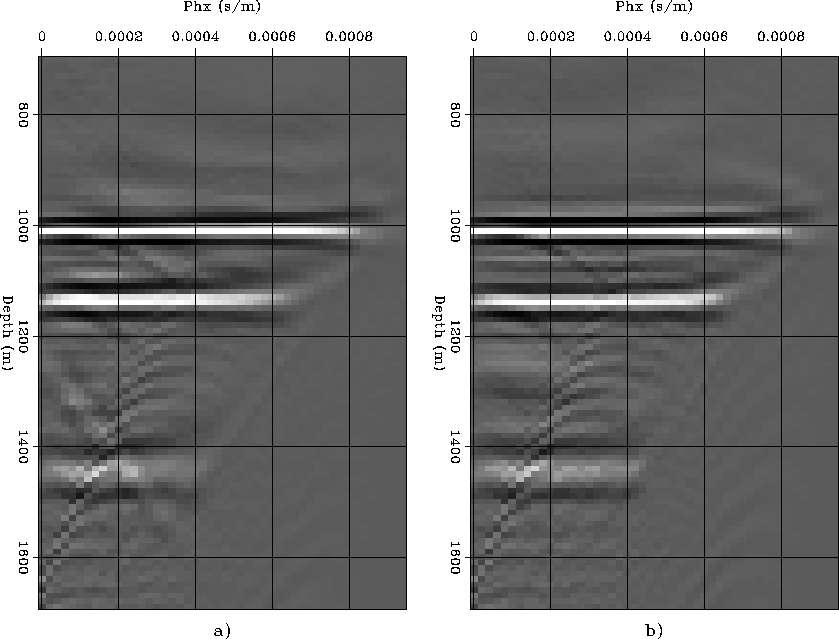
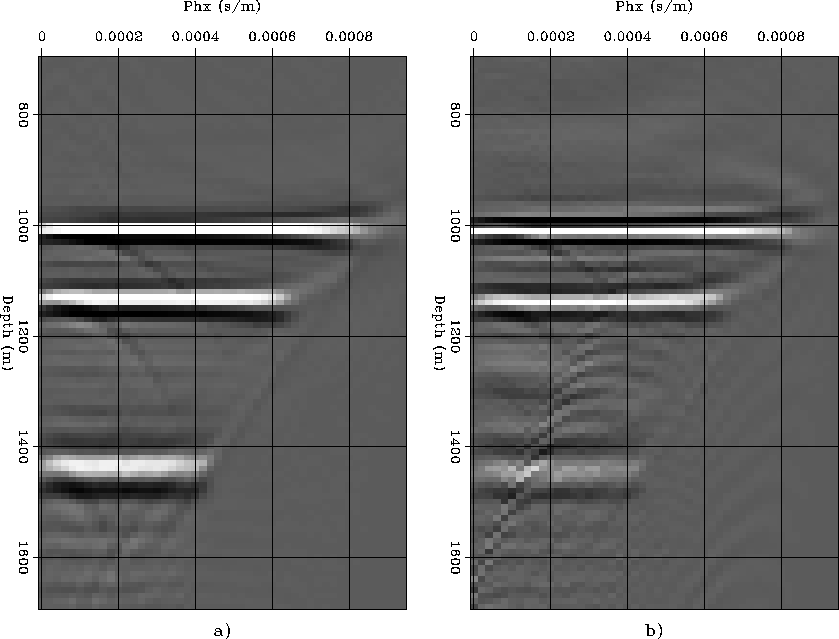
Figures 12 shows two
ADCIGs, taken at the same location
as the ADCIG in Figure 11,
but obtained with Nyh=8.
The ADCIG on the left (a) was obtained
by full phase-shift migration, and
the ADCIG on the left (a) was obtained
by the first method for narrow-azimuth migration.
For narrow azimuth-migration I used
km/s and 
km/s.
The kinematics of the narrow-azimuth migration are correct.
On the contrary, the results of full phase shift migration
begin to degrade at larger pxh.
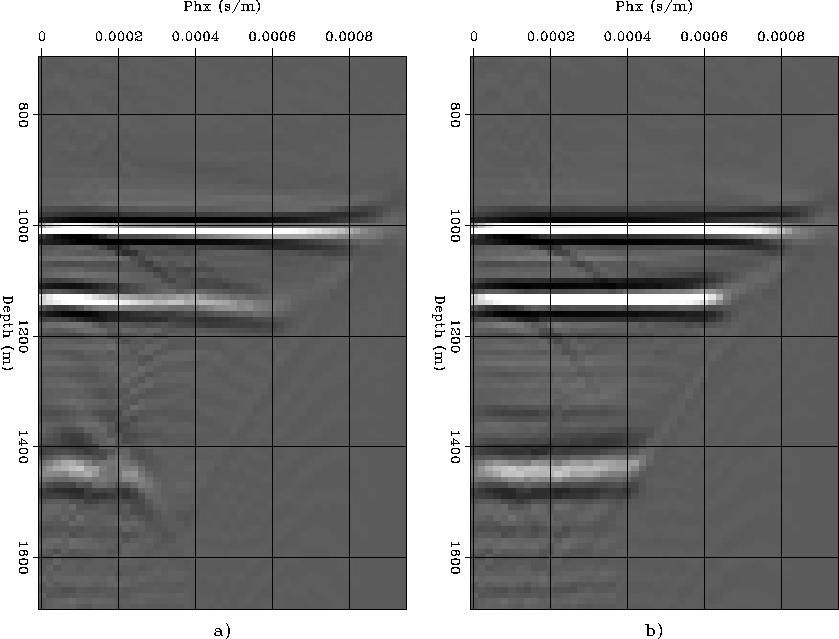
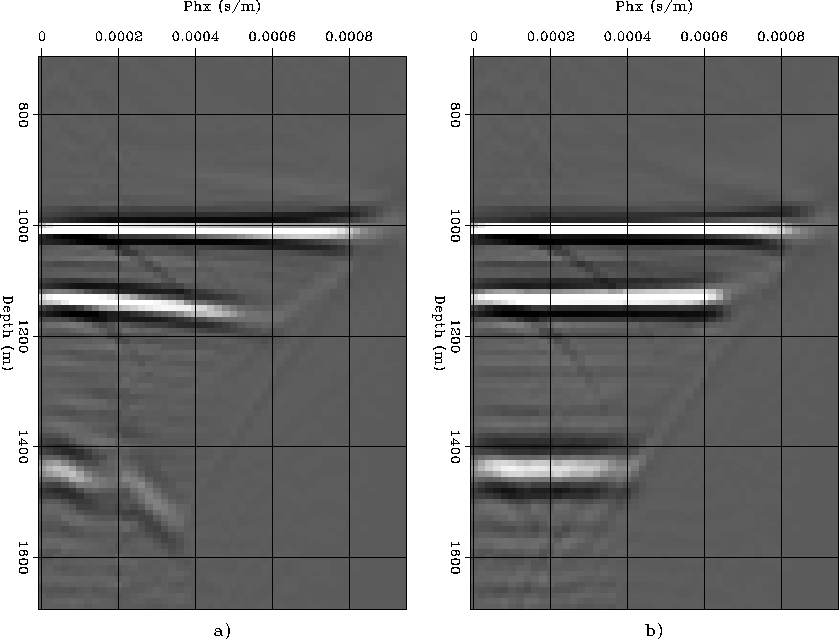
Figures 13 and 14 shows the same ADCIGs as in Figure 12, but with respectively Nyh=4 and Nyh=2. The kinematics of the narrow-azimuth migration are correct for Nyh=4 and show only a slight degradation at large pxh for Nyh=2. On the contrary, the results of full phase shift migration are poor even at small pxh.
Finally, I compare the results of using the two methods for narrow-azimuth migrations that I presented in the previous section. Figure 15 shows the ADCIGs taken at the same location as in Figure 12, also obtained with Nyh=8. The ADCIG on the left is obtained using the second narrow-azimuth method; that is, when using equation (7) to determine the sampling rate for kyh. The ADCIG on the right is obtained using the first narrow-azimuth method; that is, when using equation (6) to determine the sampling rate for kyh. The kinematics of the two images are equivalent. However, the image obtained using the second method has less artifacts caused by the boundaries along the crossline-offset axis.
|
PS-16-nhy-WKBJ-vp
Figure 10 Subset of the results of full phase-shift migration of the synthetic data set with Nyh=16. The front face of the cube is an inline section through the stack. The other two faces are sections through the prestack image. |  |
|
CIG-PS-16-nhy-WKBJ-cig
Figure 11 An ADCIG extracted from the same migrated image shown in Figure 10. The three events in the figure correspond to the planes dipping at 30, 45 and 60 degrees. Notice that the events are perfectly flat. |  |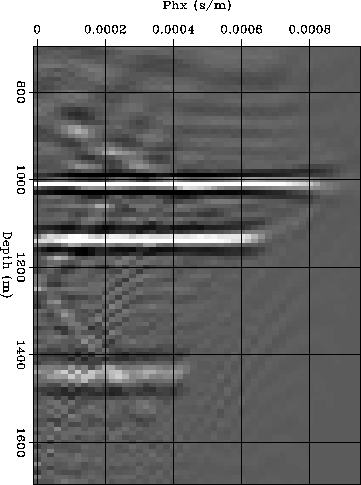
 |
 |
 |
 |