




Next: The Cauchy problem and
Up: Confirmation of offset continuation
Previous: The Kirchhoff modeling approximation
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes the process of seismogram
transformation in the time-midpoint-offset domain. In order to obtain
the high-frequency asymptotics of the equation's solution by standard
methods, we can introduce a trial asymptotic solution of the
form (
) describes the process of seismogram
transformation in the time-midpoint-offset domain. In order to obtain
the high-frequency asymptotics of the equation's solution by standard
methods, we can introduce a trial asymptotic solution of the
form (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
If we then rewrite the eikonal equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the
time-source-receiver coordinate system as (
) in the
time-source-receiver coordinate system as (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
we can easily
),
we can easily![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) verify that the explicit
expression for the phase of the Kirchhoff integral
kernel (
verify that the explicit
expression for the phase of the Kirchhoff integral
kernel (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) satisfies the eikonal equation for any
scattering point x. Here,
) satisfies the eikonal equation for any
scattering point x. Here, 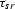 is related to
is related to 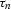 as t
is related to tn in equation (
as t
is related to tn in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
The general solution of the amplitude equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
has the form
)
has the form
| 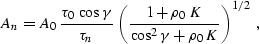 |
(214) |
which is a particular form of the previously derived
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for continuation from zero offset. Since
the kernel (
) for continuation from zero offset. Since
the kernel (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) of the Kirchhoff
integral (
) of the Kirchhoff
integral (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) corresponds kinematically to the reflection
from a point diffractor, we can obtain the solution of the amplitude
equation for this case by formally setting the curvature K to
infinity (setting the radius of curvature to zero). The infinite
curvature transforms formula (
) corresponds kinematically to the reflection
from a point diffractor, we can obtain the solution of the amplitude
equation for this case by formally setting the curvature K to
infinity (setting the radius of curvature to zero). The infinite
curvature transforms formula (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the relationship
) to the relationship
| 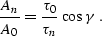 |
(215) |
Again, we exploit the assumption that
the signal f has the form of the delta function.
In this case, the amplitudes
before and after the NMO correction are connected according to the
known properties of the delta function, as follows:
| 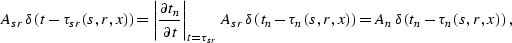 |
(216) |
with
| 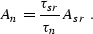 |
(217) |
Combining equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields
) yields
| 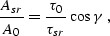 |
(218) |
which coincides exactly with the previously found
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
It is apparent that the OC differential
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the Kirchhoff representation have
the same effect on reflection data because the amplitude and phase of
the former match those of the latter. Thus, we see that the amplitude
and phase of the Kirchhoff representation for arbitrary offset
correspond to the point diffractor WKBJ solution of the
offset-continuation differential equation. Hence, the Kirchhoff
approximation is a solution of the OC differential equation when we
hold the reflection coefficient constant. This means that the
solution of the OC differential equation has all the features of
amplitude preservation, as does the Kirchhoff representation,
including geometrical spreading, curvature effects, and phase shift
effects. Furthermore, in the Kirchhoff representation and the
solution of the OC partial differential equation by WKBJ, we have not
used the 2.5-D assumption. Therefore the preservation of amplitude is
not restricted to cylindrical surfaces as it is in Bleistein's and
Cohen's 1995 true-amplitude proof for DMO.
) and the Kirchhoff representation have
the same effect on reflection data because the amplitude and phase of
the former match those of the latter. Thus, we see that the amplitude
and phase of the Kirchhoff representation for arbitrary offset
correspond to the point diffractor WKBJ solution of the
offset-continuation differential equation. Hence, the Kirchhoff
approximation is a solution of the OC differential equation when we
hold the reflection coefficient constant. This means that the
solution of the OC differential equation has all the features of
amplitude preservation, as does the Kirchhoff representation,
including geometrical spreading, curvature effects, and phase shift
effects. Furthermore, in the Kirchhoff representation and the
solution of the OC partial differential equation by WKBJ, we have not
used the 2.5-D assumption. Therefore the preservation of amplitude is
not restricted to cylindrical surfaces as it is in Bleistein's and
Cohen's 1995 true-amplitude proof for DMO.





Next: The Cauchy problem and
Up: Confirmation of offset continuation
Previous: The Kirchhoff modeling approximation
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the
time-source-receiver coordinate system as (
) in the
time-source-receiver coordinate system as (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
we can easily
),
we can easily![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) verify that the explicit
expression for the phase of the Kirchhoff integral
kernel (
verify that the explicit
expression for the phase of the Kirchhoff integral
kernel (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) satisfies the eikonal equation for any
scattering point x. Here,
) satisfies the eikonal equation for any
scattering point x. Here, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes the process of seismogram
transformation in the time-midpoint-offset domain. In order to obtain
the high-frequency asymptotics of the equation's solution by standard
methods, we can introduce a trial asymptotic solution of the
form (
) describes the process of seismogram
transformation in the time-midpoint-offset domain. In order to obtain
the high-frequency asymptotics of the equation's solution by standard
methods, we can introduce a trial asymptotic solution of the
form (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the
time-source-receiver coordinate system as (
) in the
time-source-receiver coordinate system as (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
we can easily
),
we can easily![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) verify that the explicit
expression for the phase of the Kirchhoff integral
kernel (
verify that the explicit
expression for the phase of the Kirchhoff integral
kernel (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) satisfies the eikonal equation for any
scattering point x. Here,
) satisfies the eikonal equation for any
scattering point x. Here, ![]() is related to
is related to ![]() as t
is related to tn in equation (
as t
is related to tn in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
has the form
)
has the form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for continuation from zero offset. Since
the kernel (
) for continuation from zero offset. Since
the kernel (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) of the Kirchhoff
integral (
) of the Kirchhoff
integral (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) corresponds kinematically to the reflection
from a point diffractor, we can obtain the solution of the amplitude
equation for this case by formally setting the curvature K to
infinity (setting the radius of curvature to zero). The infinite
curvature transforms formula (
) corresponds kinematically to the reflection
from a point diffractor, we can obtain the solution of the amplitude
equation for this case by formally setting the curvature K to
infinity (setting the radius of curvature to zero). The infinite
curvature transforms formula (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the relationship
) to the relationship
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields
) yields
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the Kirchhoff representation have
the same effect on reflection data because the amplitude and phase of
the former match those of the latter. Thus, we see that the amplitude
and phase of the Kirchhoff representation for arbitrary offset
correspond to the point diffractor WKBJ solution of the
offset-continuation differential equation. Hence, the Kirchhoff
approximation is a solution of the OC differential equation when we
hold the reflection coefficient constant. This means that the
solution of the OC differential equation has all the features of
amplitude preservation, as does the Kirchhoff representation,
including geometrical spreading, curvature effects, and phase shift
effects. Furthermore, in the Kirchhoff representation and the
solution of the OC partial differential equation by WKBJ, we have not
used the 2.5-D assumption. Therefore the preservation of amplitude is
not restricted to cylindrical surfaces as it is in Bleistein's and
Cohen's 1995 true-amplitude proof for DMO.
) and the Kirchhoff representation have
the same effect on reflection data because the amplitude and phase of
the former match those of the latter. Thus, we see that the amplitude
and phase of the Kirchhoff representation for arbitrary offset
correspond to the point diffractor WKBJ solution of the
offset-continuation differential equation. Hence, the Kirchhoff
approximation is a solution of the OC differential equation when we
hold the reflection coefficient constant. This means that the
solution of the OC differential equation has all the features of
amplitude preservation, as does the Kirchhoff representation,
including geometrical spreading, curvature effects, and phase shift
effects. Furthermore, in the Kirchhoff representation and the
solution of the OC partial differential equation by WKBJ, we have not
used the 2.5-D assumption. Therefore the preservation of amplitude is
not restricted to cylindrical surfaces as it is in Bleistein's and
Cohen's 1995 true-amplitude proof for DMO.