




Next: Interpolation with Fourier basis
Up: Forward interpolation
Previous: Function basis
The usual (although not unique) mathematical definition of the
continuous dot product is
| 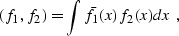 |
(38) |
where the bar over f1 stands for complex conjugate (in the case of
complex-valued functions). Applying definition (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the
dot product in equation (
) to the
dot product in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and approximating the integral
by a finite sum on the regular grid N, we arrive at the approximate
equality
) and approximating the integral
by a finite sum on the regular grid N, we arrive at the approximate
equality
| 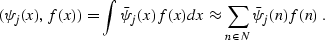 |
(39) |
We can consider equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) not only as a useful
approximation, but also as an implicit definition of the
regular grid. Grid regularity means that approximation (
) not only as a useful
approximation, but also as an implicit definition of the
regular grid. Grid regularity means that approximation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is possible. According to this definition, the more regular the grid
is, the more accurate is the approximation.
)
is possible. According to this definition, the more regular the grid
is, the more accurate is the approximation.
Substituting equality (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into equations (
) into equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and (
)
and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields a solution to the interpolation problem.
The solution takes the form of equation (
) yields a solution to the interpolation problem.
The solution takes the form of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with
) with
| 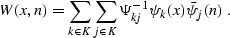 |
(40) |
We have found a constructive way of creating the linear
interpolation operator from a specified set of basis functions.
It is important to note that the adjoint of the linear operator in
formula (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is the continuous dot product of the
functions W (x, n) and f (x). This simple observation follows from
the definition of the adjoint operator and the simple equality
) is the continuous dot product of the
functions W (x, n) and f (x). This simple observation follows from
the definition of the adjoint operator and the simple equality
| 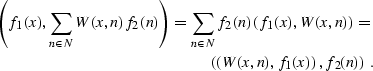 |
|
| (41) |
In the final equality, we have assumed that the discrete dot product
is defined by the sum
| 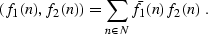 |
(42) |
Applying the adjoint interpolation operator to the function f,
defined with the help of formula (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and employing
formulas (
), and employing
formulas (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we discover that
), we discover that
| 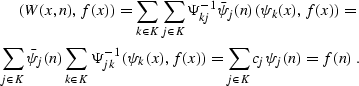 |
|
| (43) |
This remarkable result shows that although the forward linear
interpolation is based on approximation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the adjoint
interpolation produces an exact value of f (n)! The approximate
nature of equation (
), the adjoint
interpolation produces an exact value of f (n)! The approximate
nature of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) reflects the fundamental
difference between adjoint and inverse linear operators
Claerbout (1992).
) reflects the fundamental
difference between adjoint and inverse linear operators
Claerbout (1992).
When adjoint interpolation is applied to a constant function 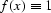 , it is natural to require the constant output f (n) = 1.
This requirement leads to yet another general property of the
interpolation functions W (x,n):
, it is natural to require the constant output f (n) = 1.
This requirement leads to yet another general property of the
interpolation functions W (x,n):
Property 9380
| 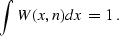 |
(44) |
The functional basis approach to interpolation is well developed in
the sampling theory Garcia (2000). Some classic examples are discussed
in the next section.





Next: Interpolation with Fourier basis
Up: Forward interpolation
Previous: Function basis
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the
dot product in equation (
) to the
dot product in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and approximating the integral
by a finite sum on the regular grid N, we arrive at the approximate
equality
) and approximating the integral
by a finite sum on the regular grid N, we arrive at the approximate
equality
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) not only as a useful
approximation, but also as an implicit definition of the
regular grid. Grid regularity means that approximation (
) not only as a useful
approximation, but also as an implicit definition of the
regular grid. Grid regularity means that approximation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is possible. According to this definition, the more regular the grid
is, the more accurate is the approximation.
)
is possible. According to this definition, the more regular the grid
is, the more accurate is the approximation.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into equations (
) into equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and (
)
and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields a solution to the interpolation problem.
The solution takes the form of equation (
) yields a solution to the interpolation problem.
The solution takes the form of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with
) with
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is the continuous dot product of the
functions W (x, n) and f (x). This simple observation follows from
the definition of the adjoint operator and the simple equality
) is the continuous dot product of the
functions W (x, n) and f (x). This simple observation follows from
the definition of the adjoint operator and the simple equality
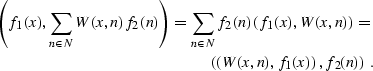
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and employing
formulas (
), and employing
formulas (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we discover that
), we discover that
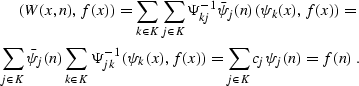
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the adjoint
interpolation produces an exact value of f (n)! The approximate
nature of equation (
), the adjoint
interpolation produces an exact value of f (n)! The approximate
nature of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) reflects the fundamental
difference between adjoint and inverse linear operators
Claerbout (1992).
) reflects the fundamental
difference between adjoint and inverse linear operators
Claerbout (1992).
![]() , it is natural to require the constant output f (n) = 1.
This requirement leads to yet another general property of the
interpolation functions W (x,n):
, it is natural to require the constant output f (n) = 1.
This requirement leads to yet another general property of the
interpolation functions W (x,n):