Let ![]() be the vector of observed data, and
be the vector of observed data, and ![]() be the
ideal underlying model. The regularized data represent the model
estimate
be the
ideal underlying model. The regularized data represent the model
estimate ![]() . Taking into account the lack of
information about
. Taking into account the lack of
information about ![]() , we can treat both
, we can treat both ![]() and
and
![]() as random vectors and approach the problem of finding
as random vectors and approach the problem of finding
![]() statistically.
statistically.
For any two random vectors ![]() and
and ![]() , let us denote by
, let us denote by
![]() the mathematical expectation of the random matrix
the mathematical expectation of the random matrix
![]() , where
, where ![]() denotes the adjoint of y.
Analogously,
denotes the adjoint of y.
Analogously, ![]() will denote the mathematical expectation
of
will denote the mathematical expectation
of ![]() . For zero-mean vectors, the matrices
. For zero-mean vectors, the matrices
![]() and
and ![]() correspond to covariances. In a
more general case, they are second-moment statistics of the
corresponding random processes.
correspond to covariances. In a
more general case, they are second-moment statistics of the
corresponding random processes.
Applying the Gauss-Markoff theorem, one can obtain an
explicit form of the estimate ![]() under three very
general assumptions Liebelt (1967):
under three very
general assumptions Liebelt (1967):
| |
(1) |
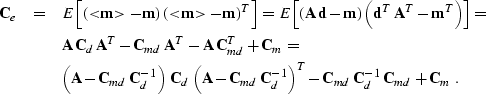 |
||
| (2) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) that Ce will be
minimized when
) that Ce will be
minimized when | |
(3) |
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) has fundamental importance in different
data regularization schemes. With some slight modifications, it
appears as the basis for such methods as optimal interpolation in
atmospheric data analysis Daley (1991); Gandin (1965), least-squares
collocation in geodesy Moritz (1980), and linear kriging in petroleum
and mining engineering Hohn (1999); Journel and Huijbregts (1978). In order to apply formula
(
) has fundamental importance in different
data regularization schemes. With some slight modifications, it
appears as the basis for such methods as optimal interpolation in
atmospheric data analysis Daley (1991); Gandin (1965), least-squares
collocation in geodesy Moritz (1980), and linear kriging in petroleum
and mining engineering Hohn (1999); Journel and Huijbregts (1978). In order to apply formula
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in practice, one needs first to get an estimate of
the matrices
) in practice, one needs first to get an estimate of
the matrices ![]() and
and ![]() . In geostatistics, the
covariance matrices are usually chosen from simple variogram models
Deutsch and Journel (1997).
. In geostatistics, the
covariance matrices are usually chosen from simple variogram models
Deutsch and Journel (1997).
Unfortunately, a straightforward application of the Gauss-Markoff
formula (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is computationally unaffordable for typical
seismic data applications. If the data vector contains N parameters,
a straightforward application will lead to an N by N matrix
inversion, which requires storage proportional to N2 and a number
of operations proportional to N3. Although the data can be divided
into local patches to reduce the computational requirements for an
individual patch, the total computational complexity is still too high
to be affordable for the values of N typical in 3-D seismic
exploration (N as high as 1010).
) is computationally unaffordable for typical
seismic data applications. If the data vector contains N parameters,
a straightforward application will lead to an N by N matrix
inversion, which requires storage proportional to N2 and a number
of operations proportional to N3. Although the data can be divided
into local patches to reduce the computational requirements for an
individual patch, the total computational complexity is still too high
to be affordable for the values of N typical in 3-D seismic
exploration (N as high as 1010).
We can take two major theoretical steps to reduce the computational complexity of the method. The first step is to approximate the covariance matrices with sparse operators so that the matrix multiplication is reduced from N2 operations to something linear in N. The second step is to approach model estimation as an optimization problem and to use an iterative method for solving it. The goal is to obtain a reasonable model estimate after only a small number of iterations.