Discussion

The example presented in this paper does not exemplify the interesting subject of scale-dependant phenomena; seismic wave propogation being one of them. In this case, the scaling is generally in terms of temporal frequency. Specifically, estimates of an earth property obtained by inversion of seismic data collected at different scales will generally be different Mavko et al. (1998). Small-scale measurements (with limited spatial coverage) of various earth properties are obtainable from well logs, while larger-scale measurements with good spatial coverage are provided by surface seismic data. In theory, the physics governing the scale dependance of the problem is known; I believe that a stronger form of multiscale regularization can effectively constrain a joint inversion of surface seismic and well log data.

The quadtree pyramid interpolation method I presented is common sensical, but has some strong theoretical justifications as well. The operator 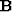$\bf B$ of equation 1 which conducts the experiment has a very simple form, and a similarly simple nullspace. The nullspace is simply all linear combinations of the unknown model points. Least squares regularization constrains the nullspace with a priori assumptions. The quadtree pyramid is slightly different. 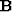Recall that there always exists a bin size such that $\bf B$ of equation 1 is invertible; the model at this scale is unique. Going to the next finest scale, we can simply fill the holes with the model estimate at the coarsest scale. In this sense, we fill the nullspace optimally in the sense that the filling is done with ``known'' data. Analogously, in spline theory, it can be shown Ahlberg et al. (1967) that the best estimator of the spline coefficients on a fine mesh are the coefficients on a coarser mesh.