 |
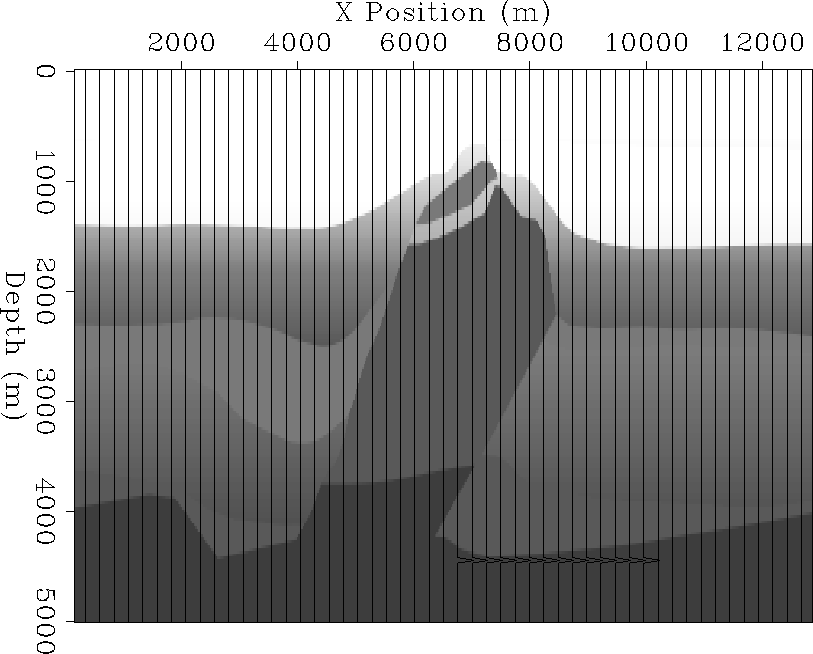
Figure 3 Synthetic model of a single, flat reflector in the Elf velocity model.
We have two goals in performing inversion rather than migration. The first is to obtain accurate amplitudes that migration would require a complicated weighting function to get. The second goal is to compensate for the limitations in our recording geometry and the effects of complex overburden that can create null spaces. By using preconditioning with our inversion problem, we hope to fill the null spaces with reasonable amplitudes.
To test the effect of preconditioning on amplitude, we created a simple, flat reflector model with a constant amplitude for all reflection angles. We then generated the data for this model by using the adjoint of the migration process explained in Prucha et al. (1999b), essentially upward continuing the wavefield through the synthetic Elf velocity model (Figure 3) with a very long half offset of 6400 meters. We chose this velocity model and reflector location because there is a shadow zone in this area Prucha et al. (1998) and should therefore create amplitude problems with simple migration.
 |
To create a "correct" answer to the amplitude question, we migrated the long offset data using wave-equation RAD migration. The extremely long offset allowed us to minimize the model null space. The resultant amplitude response along reflection angle, which is ideally constant for continuous, infinite survey geometry, we considered to be our ideal solution (panel A in Figure 4). The response is almost constant for all reflection angles but the wavelet broadens slightly with increasing angle, which is expected because of effects similar to normal moveout (NMO) stretch.
We then cut our survey geometry to one quarter of its original size by making the maximum half offset 1600 meters, which is the size of the offset in the real dataset that the synthetic model is based on. Prucha et al. (1998) has shown that with this survey geometry for this synthetic model, migration in the offset domain results in amplitudes that are very low at short and long offsets and fairly constant at mid-offsets. The AVA response obtained from RAD migration of this reduced dataset (panel C in Figure 4) is quite different from our "correct" answer. It has very low amplitudes at small angles and no response at large angles, which is not surprising given the response seen in the offset domain. There is a sharp increase in amplitude in the mid-range of the reflection angles which is clearly not correct. There even appears to be some curvature to the event, despite the fact that we know we used the correct velocity model.
Finally, we applied our preconditioned inversion to the limited offset data (panel B in Figure 4). Although the response is not perfect, it is closer to our "correct" response after only one iteration. It is a nice, smooth response that does not vary as much with angle as the migration result. It is still weak at small and large angles, but it extends farther into the large angles than does the short-offset migration. It is also flat, like the ideal response.
 |