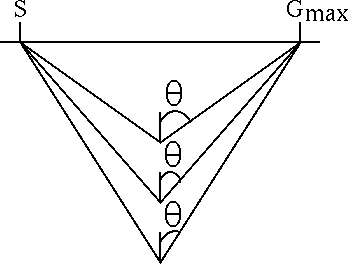Creating common image gathers (CIGs) in the RAD can be done by Kirchhoff methods Xu et al. (1998) or wave-equation methods Prucha et al. (1999a). However, there are issues in both that must be taken into account to properly image the subsurface and handle the amplitudes intelligently.
The RAD has some inherent limitations caused by our finite survey geometries. One of these is a depth dependency. As depth increases, the maximum reflection angle that can be imaged decreases (Figure 1). This creates a null space that increases with depth. It is also easy to see that the maximum reflection angle that can be imaged for a particular point in the subsurface is dependent on the dip of the reflector being imaged (Figure 2), so the model null space is less predictable than a simple function of depth.
|
depth
Figure 1 Depth limitation of maximum reflection angle imaged. |  |
|
dip
Figure 2 Dip limitation of maximum reflection angle imaged. The dashed lines relate to the zero dip reflector, the solid lines to the dipping reflector. The maximum reflection angle possible for the dipping reflector is much smaller than that for the zero dip reflector. |  |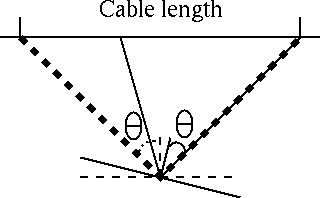
It is clear that these limitations will result in missing data where the energy from a reflector within the survey area arrives at the surface at a point outside of the survey geometry. This is especially troublesome in complex areas with rapidly varying velocity, where the behavior can vary quickly spatially. This "missing" data will create a model null space. We want to fill this null space intelligently, so we turn to inversion.
Another reason inversion is superior to migration in complex areas is that it is easier to get accurate amplitudes. In areas where the subsurface is simple, obtaining reasonable amplitudes is easy to do with almost any migration method. As the problem becomes more complex, correctly weighting arrivals becomes essential Albertin et al. (1999); Bloor et al. (1999). For the complex environments that the reflection angle domain is most useful in, the weighting function that would have to be applied to the migration process is very difficult to find, let alone code effectively. When we use inversion, our problem converges to give us accurate amplitudes without needing the additional weighting function, so the problem is less complex than the migration problem would be to get an equivalent answer.