To construct the 3-D steering filter operator I followed
the methodology described in Clapp (2000), cascading
two 2-D steering filter operators to form my 3-D steering filter operator.
I used the
five reflectors picked in the last section. To calculate
the dip field I began by calculating the slope in the x-z and y-z planes.
I mapped these two dip fields into ![]() model space.
I then interpolated the field to the entire model space.
model space.
I then interpolated the field to the entire model space.
Once I had the dips in both the x-z and y-z planes I constructed
two filter banks which encompassed the range of dips in each direction.
It was then a simple matter of creating a mapping operator that
mapped the dip at a given model point to a specific filter in the bank.
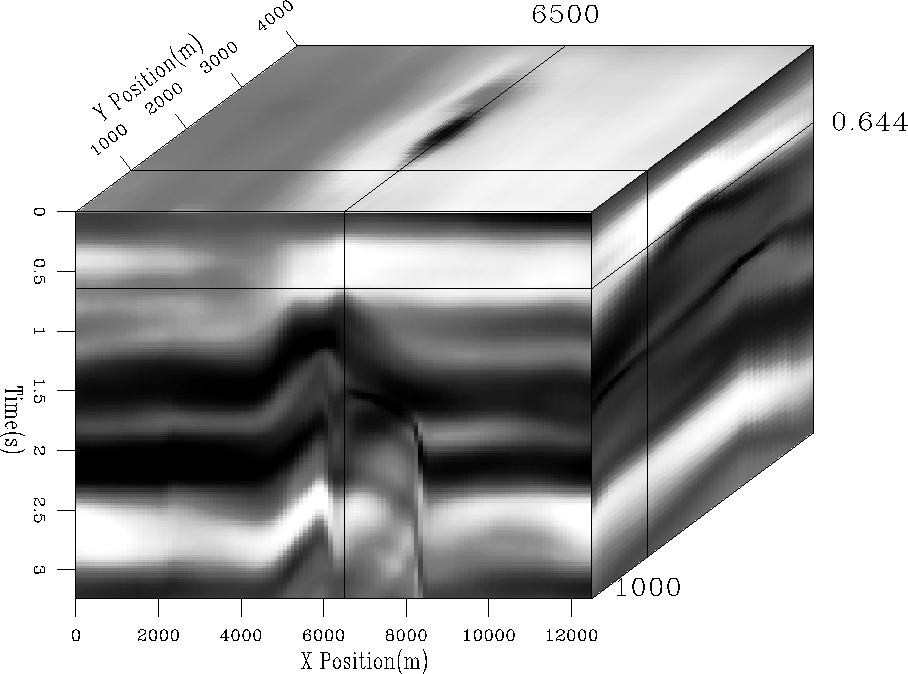
To see the effect of this new complex operator I filled the model
with random noise and then applied A3dA3d'
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). As you can see the 3-D steering
filter does a good job in spreading energy along reflector directions.
). As you can see the 3-D steering
filter does a good job in spreading energy along reflector directions.
 |