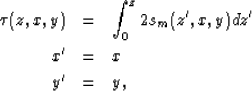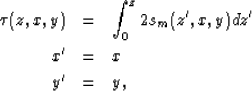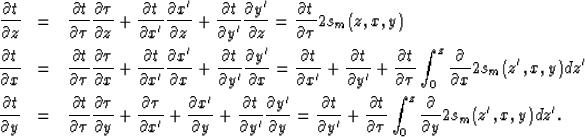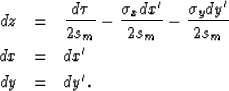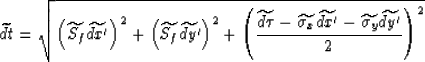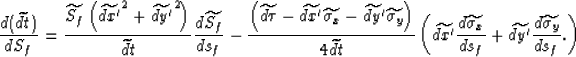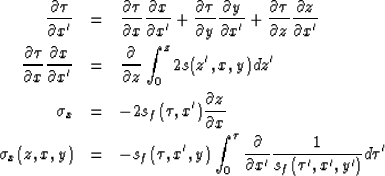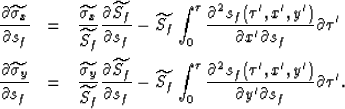Next: Data
Up: Clapp: 3-D tomography field
Previous: Review
To construct 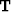 we must derive a relationship between dt and
we must derive a relationship between dt and
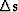 . We will begin by defining two different slownesses: focusing
and mapping slowness. The focusing slowness is the slowness that best
focuses the data. The mapping slowness is the slowness that correctly
positions the data.
. We will begin by defining two different slownesses: focusing
and mapping slowness. The focusing slowness is the slowness that best
focuses the data. The mapping slowness is the slowness that correctly
positions the data.
Starting with mapping slowness sm in terms of x,y, and z, we
can transform into tau space through
| 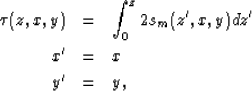 |
|
| (5) |
| |
where  is the two-way vertical traveltime, x' is our new x coordinate, and
y' is our new y coordinate.
Using the chain rule we can derive the relationship between
the derivatives of our coordinates,
is the two-way vertical traveltime, x' is our new x coordinate, and
y' is our new y coordinate.
Using the chain rule we can derive the relationship between
the derivatives of our coordinates,
| 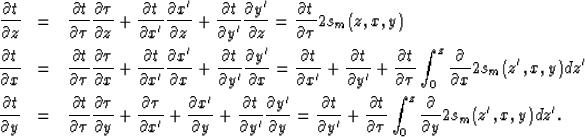 |
(6) |
| (7) |
| (8) |
We can simplify the above relations by defining two  quantities,
one in the x-direction,
quantities,
one in the x-direction, 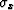 , and one in the y-direction,
, and one in the y-direction,
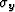 ,
,
| 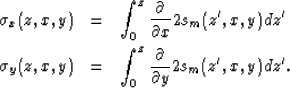 |
(9) |
| (10) |
Taking the derivative of both sides of the transform of (5)
we can obtain a relation for dz, dx, and dy,
| 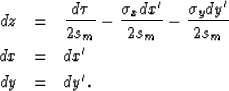 |
(11) |
| (12) |
| (13) |
To obtain our tomography operator in 3-D we begin by defining the
traveltime along a single ray segment
(where quantities measured along the ray segment are indicated by ) in tau space using equations
(11-13),
| 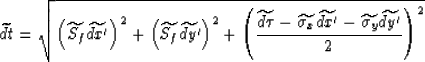 |
(14) |
We can then take the derivative with respect to the focusing slowness sf,
| 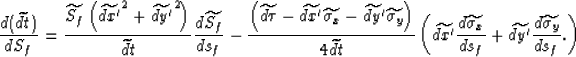 |
(15) |
We new have an expression in terms of 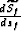 ,
,
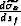 , and
, and 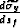 .To get an expression in terms of just
.To get an expression in terms of just 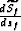 we start by taking the partial derivative of
we start by taking the partial derivative of  with respect to x',
with respect to x',
| 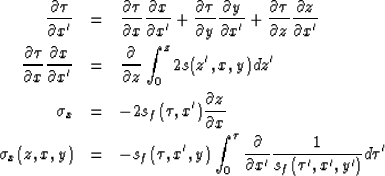 |
(16) |
| |
| |
| |
and similarly
| 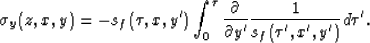 |
(17) |
We then take the derivative with respect to sf and evaluate at the
ray segment,
| 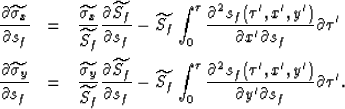 |
(18) |
| (19) |
As a result we now have a linear relation between
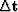 and Sf in the tau domain.
and Sf in the tau domain.





Next: Data
Up: Clapp: 3-D tomography field
Previous: Review
Stanford Exploration Project
9/5/2000