Introduction

Preserving the amplitudes requires inverse theory when an operator is not unitary. Unfortunately, seismic operators are usually not unitary. Seismic operators can be regarded as the adjoint of forward ``modeling'' operators Claerbout (1992). Lailly (1983) was the first to recognize that the standard migration operator is the adjoint to the corresponding forward operator and used it in the first iteration of full waveform inversion Tarantola (1987). Because the adjoint is not the inverse of the operator, the amplitude of the input data is not preserved. An approximate inverse can be computed using least-squares inversion. Thorson (1984) replaces the standard hyperbolic Radon transform with a linear, least-squares inversion of the velocity stack equations. However, the least-squares operator involves the computing of the inverse of the Hessian that is often very difficult to derive. Forgues and Lambare (1997) and Chavent and Plessix (1999) calculated an approximate inverse of the Hessian matrix associated with the migration operator. When the calculation of the least-squares inverse is not feasible (size of the matrices, use of operators instead of matrices), an iterative scheme is preferred.

However, with a least-squares inversion, major difficulties arise when the data are contaminated by noisy events. By noisy event I mean

• Abnormally large or small data components, or outliers, where long-tailed probability density functions (pdf) should be used as opposed to short-tailed Gaussian pdf.
• Coherent noise that the seismic operator is unable to model (for example, a hyperbolic Radon transform can't properly model ellipses).

The noise will (1) spoil any analysis based on the result of the inversion and (2) affect the amplitude recovery of the input data. From a more statistical point of view, the residual, which measures the quality of the data fitting, will be corrupted by high amplitude (outliers in the data) or highly correlated events (coherent noise in the data) that will attract much of the solver's efforts, thus degrading the model m. The first I in IID stands for Independent, meaning that no coherent events are present in the residual (hyperbolas, ellipses, lines, etc.). The second I and D stand for Identically Distributed, meaning that the residual components have similar energy. 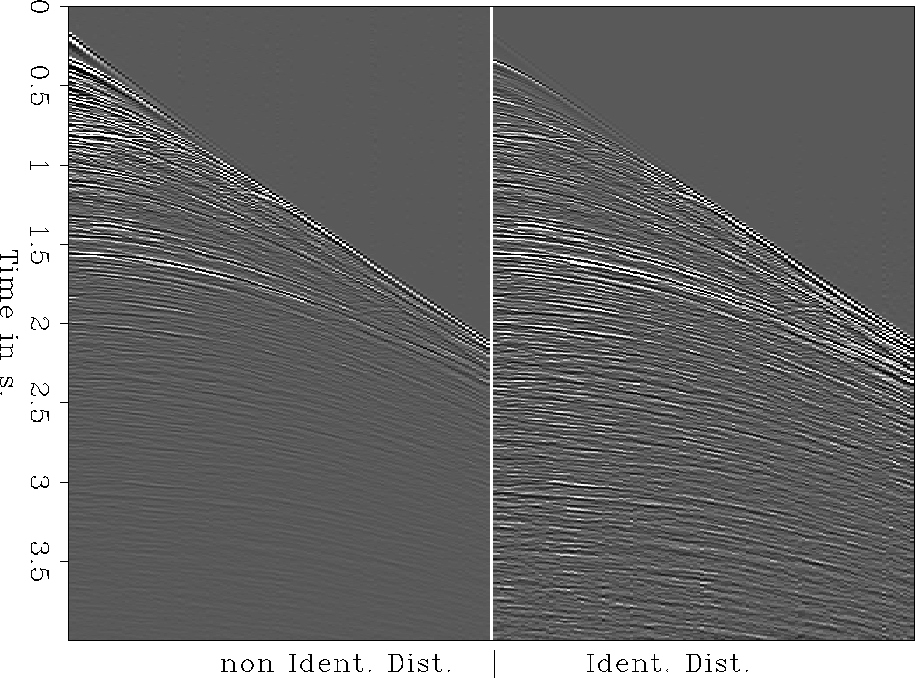For example, if seismic data have not been multiplied by t² to correct for spherical divergence effects, the variables in the gather will not be Identically Distributed (Figure ).

 

iid
Figure 1 Left: the data have not been multiplied by t² thus giving non Identically Distributed variables. Right: after t² correction, the data are Identically Distributed.

A possible solution to one particular noise problem is to attribute long-tailed pdfs to the residual variables. This long-tailed pdfs lead to the minimization of the l¹ norm of the data residual

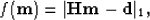$$f({\bf m}) = \vert{\bf Hm - d}\vert _1,$$ (1)

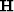where ${\bf H}$ is the seismic operator, 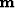${\bf m}$ the model and 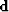${\bf d}$ the input seismic data. Because the l¹ norm is less sensitive to outliers, it will give a better fitting of the data Claerbout and Muir (1973). The minimization of such objective functions is a cumbersome problem because the l¹ norm is not differentiable everywhere. However, some alternatives exist if we use a hybrid l¹-l² norm such as the Huber norm Guitton and Symes (1999); Huber (1973) or an Iteratively Reweighted Least Squares (IRLS) algorithm Bube and Langan (1997); Nichols (1994) with an appropriate weighting function. These methods have proved efficient Guitton (2000a). The use of long-tailed pdfs is particularly effective at attenuating outliers. However, they are usually not effective at attenuating coherent noise because it is not generally distinguishable by its histogram, but by its moveout patterns. In addition, hybrid solvers are either difficult to tune or expensive to use.