In order for the PEF to contain the inverse of the data spectrum, it has to be causal. The notion of causality is most obvious when there is a single axis labeled ``time,'' but it extends readily enough to two or more dimensions. Your eye scans the page from left to right and top to bottom; the words previous to the current one are to the left on the same line and everywhere on the lines above. This gives a sort of two-dimensional causal region. Including all the words on previous pages gives a sort of three-dimensional causal region. This is somewhat arbitrary. In some other language the fast and slow axes might be swapped or reversed. The important thing is that along a line parallel to any axis and going through the current point (the zero lag, the value 1z0 in equation pefdef), a causal region lies only to one side of the current location. Figure causal shows an illustration of a two-dimensional causal region. We can make a causal prediction of the data value in the square labeled ``1'' from any or all of the other shaded squares. The shaded squares are labeled to show the layout of of a PEF with four adjustable coefficients. The ``1'' is the value 1z0 in equation pefdef, and the a(n) are the adjustable coefficients.
 |
Figure 2dpef shows a picture of a 2-D PEF, and Figure 3dpef shows a picture of a 3-D PEF. In both cases, the dark shaded block holds the 1, and the lighter blocks are the coefficients a(n) calculated from the data.
|
2dpef
Figure 2 Form of a 2-D prediction error filter. The shaded box holds the zero-lag coefficient, with a fixed value of 1. |  |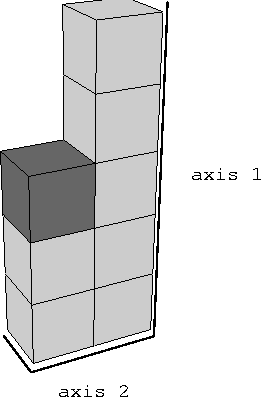
|
3dpef
Figure 3 Form of a 3-D prediction error filter. The shaded box holds the zero-lag coefficient, with a fixed value of 1. | 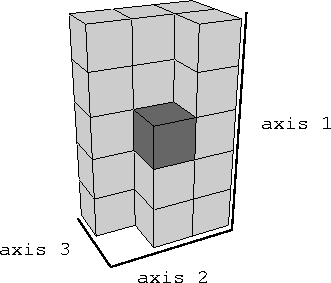 |