




Next: Causality in multiple dimensions
Up: Prediction error filters
Previous: Prediction error filters
PEFs have the important property that they whiten the data
they are designed on.
Since time-domain convolution is frequency-domain multiplication,
this implies that the PEF has a spectrum which is inverse of the
input data.
This property of PEFs is what makes the interpolation scheme described
in this thesis function.
There are various ways to prove the whitening property of PEFs;
here I follow Jain 1989 and Leon-Garcia 1994.
The minimum mean square error prediction of the 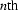 value in a stationary zero-mean data series u(n),
based on the previous p data values, is
value in a stationary zero-mean data series u(n),
based on the previous p data values, is
| 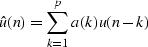 |
(1) |
The coefficients a(n) make up the bulk of the
prediction error filter for u(n), which is defined in the
Z-transform domain by
| 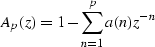 |
(2) |
The coefficients a(n) generate a prediction of the data.
Convolving the entire prediction error filter pefdef
on the input yields the prediction error 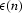 ,which is then just the difference between the estimate
,which is then just the difference between the estimate 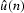 and the known data u(n).
and the known data u(n).
| 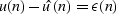 |
(3) |
The filter coefficients a(n) are determined from the
input data u(n) by minimizing the
mean square of the prediction error 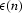 .
.
A fundamental principle from estimation theory says that the
minimum mean square prediction error is orthogonal
to the known data and to the prediction.
It turns out that this implies the most important property
of PEFs, and their utility in finding missing data.
First, to develop the orthogonality condition,
we consider the data u(n) and the estimate 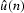 as random variables.
The estimate is the expectation of the true data u(n) based on the
rest of the data, the random sequence
as random variables.
The estimate is the expectation of the true data u(n) based on the
rest of the data, the random sequence
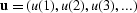 , not including u(n).
Taking
, not including u(n).
Taking 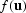 to be any function of
to be any function of  ,and using
,and using ![$E\left[\right]$](img12.gif) to denote expectation,
we can write
to denote expectation,
we can write
| ![\begin{eqnarray}
E\left [ \hat{u}(n) f(\bold u) \right] & = & E\left [ E(u(n)\ve...
...)\vert\bold u) \right ]\\ & = & E\left [ u(n) f(\bold u) \right ]\end{eqnarray}](img13.gif) |
(4) |
| (5) |
| (6) |
Since 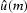 and u(m) are functions of
and u(m) are functions of  ,that implies the orthogonality conditions
,that implies the orthogonality conditions
| ![\begin{displaymath}
E \left [ (u(n) - \hat{u}(n) ) u(m) \right ] = E\left [ \epsilon(n) u(m) \right ] = 0 , \quad \quad m \neq n\end{displaymath}](img15.gif) |
(7) |
and
| ![\begin{displaymath}
E \left [ (u(n) - \hat{u}(n) ) \hat{u}(m) \right ] = E\left [ \epsilon(n) \hat{u}(m) \right ] = 0, \quad \quad m \neq n.\end{displaymath}](img16.gif) |
(8) |
With certain provisos, these orthogonality conditions imply that the prediction error is white:
| ![\begin{displaymath}
E\left[\epsilon(n)\epsilon(m)\right] = \sigma_\epsilon^2\delta(n-m)\end{displaymath}](img17.gif) |
(9) |
where 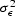 is the variance of
is the variance of 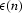 .
.
For proof, replace n with m-k, and
| ![\begin{eqnarray}
E \left [ \epsilon(m) \epsilon(m-k) \right ] & = & E \left ( \l...
...(m-k) \right ] - E \left [ \epsilon(m) \sum_i a(i)u(n-k-i) \right]\end{eqnarray}](img19.gif) |
(10) |
| (11) |
The first term on the right side of equation thingy is a delta function with amplitude equal to the variance
of the prediction error, because
| ![\begin{eqnarray}
E\left[\epsilon(m)u(m)\right] & = & E\left[\epsilon(m)\epsilon(...
...(m)\sum_i a(i)u(m-i)\right] \\ & = & \sigma_\epsilon^2 , i \neq 0\end{eqnarray}](img20.gif) |
(12) |
| (13) |
| (14) |
The second term in the RHS of equation thingy is basically the same,
but the delta function appears inside the sum.
Rewriting the RHS, equation thingy turns into
| ![\begin{displaymath}
E \left [ \epsilon(m) \epsilon(m-k) \right ] = \sigma_\epsilon^2\delta(k) - \sigma_\epsilon^2\sum_i a(i)\delta(k+i)\end{displaymath}](img21.gif) |
(15) |
If the filter Ap is causal, then i = 1, 2, 3,...,p.
The sum in the RHS of equation thingy2 is zero, because k is
an autocorrelation lag, meaning 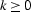 .This means the prediction error is white:
.This means the prediction error is white:
| ![\begin{displaymath}
E \left [ \epsilon(m)\epsilon(m-k) \right ] = \sigma_\epsilon^2\delta(k).\end{displaymath}](img23.gif) |
(16) |
If the filter Ap is not causal but has i =-p,...,0,...,p,
then the sum does not vanish, and the prediction error is not white.
In this case, using a(0) = -1 to fit with equation pefdef,
| ![\begin{displaymath}
E \left [ \epsilon(m)\epsilon(m-k) \right ] = - \sigma_\epsilon^2\sum_{i=-p}^{p}a(i)\delta(k+i)\end{displaymath}](img24.gif) |
(17) |
The prediction error is the output of the convolution
of PEF and data, so if the prediction error is white,
then the PEF spectrum tends to the inverse of the data spectrum.
This is the most important thing about PEFs; they give
an estimate of the inverse data spectrum.
This is only true for a causal prediction.
The development above uses one-dimensional data series.
In this thesis I deal with predicting missing trace data
from other known traces,
so two and more dimensions are necessary.
Thinking in helical coordinates Claerbout (1998) allows
extension to arbitrarily many dimensions.
Jain 1989 develops the same
arguments with more dimensions.
Also, Claerbout 1997 gives alternative
whiteness proofs in one dimension and two dimensions, attributed to
John Burg.





Next: Causality in multiple dimensions
Up: Prediction error filters
Previous: Prediction error filters
Stanford Exploration Project
1/18/2001
![]() value in a stationary zero-mean data series u(n),
based on the previous p data values, is
value in a stationary zero-mean data series u(n),
based on the previous p data values, is
![]() ,which is then just the difference between the estimate
,which is then just the difference between the estimate ![]() and the known data u(n).
and the known data u(n).
![]() as random variables.
The estimate is the expectation of the true data u(n) based on the
rest of the data, the random sequence
as random variables.
The estimate is the expectation of the true data u(n) based on the
rest of the data, the random sequence
![]() , not including u(n).
Taking
, not including u(n).
Taking ![]() to be any function of
to be any function of ![]() ,and using
,and using ![]() to denote expectation,
we can write
to denote expectation,
we can write
![\begin{eqnarray}
E\left [ \hat{u}(n) f(\bold u) \right] & = & E\left [ E(u(n)\ve...
...)\vert\bold u) \right ]\\ & = & E\left [ u(n) f(\bold u) \right ]\end{eqnarray}](img13.gif)
![\begin{eqnarray}
E \left [ \epsilon(m) \epsilon(m-k) \right ] & = & E \left ( \l...
...(m-k) \right ] - E \left [ \epsilon(m) \sum_i a(i)u(n-k-i) \right]\end{eqnarray}](img19.gif)
![\begin{eqnarray}
E\left[\epsilon(m)u(m)\right] & = & E\left[\epsilon(m)\epsilon(...
...(m)\sum_i a(i)u(m-i)\right] \\ & = & \sigma_\epsilon^2 , i \neq 0\end{eqnarray}](img20.gif)
![\begin{displaymath}
E \left [ \epsilon(m)\epsilon(m-k) \right ] = - \sigma_\epsilon^2\sum_{i=-p}^{p}a(i)\delta(k+i)\end{displaymath}](img24.gif)