




Next: Radial smoothing
Up: Crawley: Nonstationary filtering
Previous: INTRODUCTION
A standard formulation for calculating PEFs from known data is
to solve a linear least-squares problem like
| 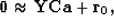 |
(1) |
where  is a vector containing the PEF coefficients,
is a vector containing the PEF coefficients,
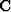 is a filter coefficient selector matrix,
and
is a filter coefficient selector matrix,
and 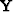 denotes convolution with the input data.
The coefficient selector
denotes convolution with the input data.
The coefficient selector 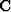 is like an identity
matrix, with a zero on the diagonal placed to prevent the
fixed 1 in the zero lag of the PEF from changing.
The
is like an identity
matrix, with a zero on the diagonal placed to prevent the
fixed 1 in the zero lag of the PEF from changing.
The 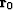 is a vector that holds the initial value
of the residual,
is a vector that holds the initial value
of the residual, 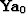 .If the unknown filter coefficients are given initial values
of zero, then
.If the unknown filter coefficients are given initial values
of zero, then 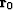 contains a copy of the input data.
contains a copy of the input data.
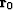 makes up for the fact that the 1 in the zero
lag of the filter is not included in the convolution (it is
knocked out by
makes up for the fact that the 1 in the zero
lag of the filter is not included in the convolution (it is
knocked out by 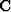 ).
).
When there are many coefficients, as when PEFs are spread
densely on the data grid, it makes sense to add damping
equations and/or precondition the problem.
Inserting the preconditioned variable 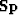 (where
(where
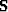 is a somewhat arbitrary smoother) for
is a somewhat arbitrary smoother) for  and
adding the also somewhat arbitrary roughener
and
adding the also somewhat arbitrary roughener 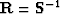 to regularize the model, gives a formulation like
to regularize the model, gives a formulation like
| 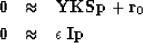 |
(2) |
| (3) |
In many cases we can set 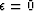 and just use equation goodleak2,
being careful not to let it go for too many iterations.
We still have to define
and just use equation goodleak2,
being careful not to let it go for too many iterations.
We still have to define 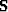 (or
(or 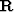 ).
).





Next: Radial smoothing
Up: Crawley: Nonstationary filtering
Previous: INTRODUCTION
Stanford Exploration Project
4/27/2000
![]() (where
(where
![]() is a somewhat arbitrary smoother) for
is a somewhat arbitrary smoother) for ![]() and
adding the also somewhat arbitrary roughener
and
adding the also somewhat arbitrary roughener ![]() to regularize the model, gives a formulation like
to regularize the model, gives a formulation like
![]() and just use equation goodleak2,
being careful not to let it go for too many iterations.
We still have to define
and just use equation goodleak2,
being careful not to let it go for too many iterations.
We still have to define ![]() (or
(or ![]() ).
).