Preprocessing and common-azimuth migration

The wave-equation approach obliges us to transform the 3-D data acquired with complex irregular geometry to regularly space-sampled data because CAM operates in the frequency-wavenumber domain and requires Fourier transforms along all axes. In contrast, Kirchhoff algorithms can handle irregular geometries without such preprocessing because they operate sequentially in a trace-by-trace manner.

Here, data regularization is performed by an operator called AMO or Azimuth Moveout Biondi et al. (1998). It also allows a local coherent stack that will reduce data volume. AMO, however, has a non-negligible computational cost in the whole imaging process (about 10% of migration cost). Effectively, introduced as the cascade of DMO and inverse DMO, AMO is a partial migration operator. With less accuracy, one can instead use a simple normalized binning procedure.

The processing scheme begins by creating a 5-axis time-midpoint-offset grid ($t, \vec{m}, \vec{h}$) for the data volume. Then, we apply a simple sequence NMO/AMO/$\mbox{NMO}^{-1}$ to regularize the data on the grid. This gridding procedure concurrently allows data resampling in common-midpoint and offset at the limit of aliasing, thus reducing further the cube dimensions and lower migration computational cost.

Marine data are usually concentrated within a narrow range of azimuth, as opposed to land data. Here, besides regularizing data along space axes, we use AMO to sum data coherently over the cross-line offset axis h_y; conventionally, the subscripts x and y refer to the in-line and the cross-line direction, respectively. Thus, we obtain 4-D common-azimuth data, for which h_y=0. After transformation to the frequency-wavenumber domain, this 4-D common-azimuth regularized dataset $D(\omega,\vec{k_m},k_{hx})$ is the wavefield recorded at depth z=0, to which CAM is applied.

Migration is then performed iteratively through common-azimuth downward-continuation of the wavefield Biondi and Palacharla (1996). The common-azimuth downward-continuation operator is derived from the stationary-phase approximation of the full 3-D prestack downward continuation operator. For more accuracy with lateral velocity variations, we use several reference velocities and interpolation as in the extended split-step method Stoffa et al. (1990). The following chart summarizes the preprocessing and imaging schemes:

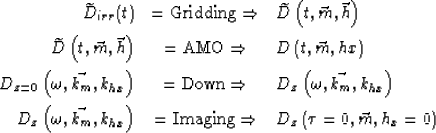$$\begin{eqnarray} \widetilde{D}_{irr}(t) & = \mbox{Gridding} \Rightarrow & \widet... ...ng} \Rightarrow & D_z\left( \tau=0,\vec{m},h_x=0 \right) \nonumber\end{eqnarray}$$

In this chart, $\widetilde{D}$ refers to data as an irregular set of traces, whereas D means data are a regular n-D cube.