




Next: REFERENCES
Up: Claerbout: Sparse PEF estimation
Previous: THE TEST CASE
How are we going to get the PEF?
I propose we invoke stationarity and scale invariance.
Notice that we have an interesting kind of scale invariance here.
We can expand the correct PEF and it is still a correct PEF.
(It is interesting to notice that an apparent scale
or resonant spectrum visible along the observation track
does not prevent the 2-D function from being scale invariant).
We have a non-linear optimization problem to solve.
You know it, 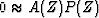 where a0=1 and some
of the pi are known.
It is non-linear.
This problem is linearized
in Claerbout (1992)
and Claerbout (2000) but I don't trust an ignorant descent.
I've had some disappointments doing that
(but that was before I learned about scale invariance).
How would you try?
where a0=1 and some
of the pi are known.
It is non-linear.
This problem is linearized
in Claerbout (1992)
and Claerbout (2000) but I don't trust an ignorant descent.
I've had some disappointments doing that
(but that was before I learned about scale invariance).
How would you try?





Next: REFERENCES
Up: Claerbout: Sparse PEF estimation
Previous: THE TEST CASE
Stanford Exploration Project
4/27/2000
![]() where a0=1 and some
of the pi are known.
It is non-linear.
This problem is linearized
in Claerbout (1992)
and Claerbout (2000) but I don't trust an ignorant descent.
I've had some disappointments doing that
(but that was before I learned about scale invariance).
How would you try?
where a0=1 and some
of the pi are known.
It is non-linear.
This problem is linearized
in Claerbout (1992)
and Claerbout (2000) but I don't trust an ignorant descent.
I've had some disappointments doing that
(but that was before I learned about scale invariance).
How would you try?