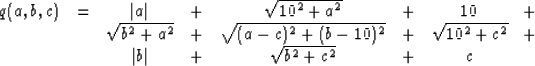What is the L1 norm of the 2-D gradient?

The idea of finding smooth solutions is to minimize a measure of the gradient. The first time I thought about doing this with L₁, I tried the wrong approach (and that put me off the track for 25 years). The wrong approach is to take the L₁ norm of the x-component of the gradient and add it to the L₁ norm of the y-component of the gradient. This is bad because it embeds the orientation of the coordinate system. Axiomatically, in science we like solutions that are independent of the human choice of a coordinate system. Thus L₁ appears to conflict with this basic requirement.

An approach independent of coordinate rotation and translation on a grid is to minimize

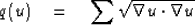$$q(u) \quad =\quad\sum \sqrt{ \nabla u \cdot \nabla u}$$ (8)

where u=u(x,y) and where the summation is over (x,y)-space. Multivariate L₁-norm problems generally reduce to a line search that is a weighted median. Hoare's algorithm makes this very fast. Unfortunately, this multidimensional generalization of L₁ does not seem to reduce to a weighted median so Hoare's algorithm is irrelevant, as might be other L₁ experiences we have seen in 1-D.

I discussed the 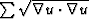$\sum \sqrt{ \nabla u \cdot \nabla u}$criterion for a while with Bill Symes. We came up with this simple problem where we would use zero side boundaries and seek the response of an impulse in the medium.

                    0  0  0  0  
                    0  a 10  0  
                    0  b  c  0  
                    0  0  0  0

The free variables are a, b, and c. We take the x derivative diagonally to the northeast and the y derivative diagonally to the southeast.

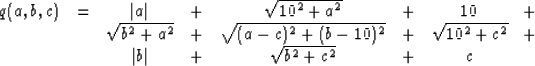$$\begin{array} {ccccccccc} q(a,b,c) &=& \vert a\vert &+& \sq... ...} &+& \\ && \vert b\vert &+& \sqrt{b^2 +c^2} &+& c\end{array}$$ (9)

A few manual calculations quickly convinced us that the solution is a=b=c=0. Thus multidimensional L₁ does not look like the answer we seek. It looks like the boundaries at infinite distance dominate the data (in this case the 10). Thus, the response to an isolated collection of spikes, might simply be the spike values where they are given and zero elsewhere.