




Next: Curve through two points
Up: EXAMPLES
Previous: Best fitting straight line
An important example
is the estimation of source and receiver time corrections.
Here one has a set of observed traveltimes
from the ith source to the jth receiver.
After known systematic geometrical and velocity effects are removed,
the time residual matrix tij remains.
Then,
near-source traveltimes si and near-receiver traveltimes rj
are estimated from the tij by minimizing the error eij
in
A trivial nonuniqueness is that
an arbitrary constant added to all the si
and subtracted from all the rj will give the same residuals.
I was surprised to discover deeper nonuniqueness lurking in
a simple example.
Absolute error minimization reduced a 3-by-3 matrix
of tij to the eij residual matrix
| ![\begin{displaymath}
e_{ij} = \left[ \begin{array}
{rrr}
0& -12 & 4 \\ 17& 0 & 0 \\ 0& 10 & 0
\end{array} \right].\end{displaymath}](img2.gif) |
(3) |
As expected theoretically (by the solution method I used),
there are 5 zeros representing the 5 independent unknowns of the 6 unknowns.
Note that 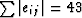 .Now modify source and receiver times
by applying +12 to row 1 and -12 to column 1.
We have
.Now modify source and receiver times
by applying +12 to row 1 and -12 to column 1.
We have
| ![\begin{displaymath}
\left[ \begin{array}
{rrr}
0 & 0 & 16 \\ 5 & 0 & 0 \\ -12 & 10 & 0
\end{array} \right],\end{displaymath}](img4.gif) |
(4) |
still with 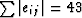 .Now apply +12 to row 3 and -12 to column 3.
We have
.Now apply +12 to row 3 and -12 to column 3.
We have
| ![\begin{displaymath}
\left[ \begin{array}
{rrr}
0 & 0 & 4 \\ 5 & 0 & -12 \\ 0 & 22 & 0
\end{array} \right].\end{displaymath}](img5.gif) |
(5) |
Furthermore, we can generate an infinite set of eij
(and hence source and receiver corrections)
all with the same 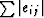 by taking residuals
(3)-(5)
and forming any convex combination
(weighted combination where each weight is positive
and the weights sum to one).
by taking residuals
(3)-(5)
and forming any convex combination
(weighted combination where each weight is positive
and the weights sum to one).
The existence of a sizeable nonuniqueness with absolute error minimization
leaves us the uncomfortable feeling that the mathematical uniqueness
of squared error is not genuine, i.e.,
that the uniqueness of results with squared error
is not a realistic charactorization of our certainty.
Often, however, the this unfamiliar nonuniqueness does not arise.
It depends on the data, not the mathematical structure of the problem.
For example,
I don't know any other minimum L1 solutions with the eij matrix:
| ![\begin{displaymath}
\left[ \begin{array}
{rrr}
0 & 0 & 0 \\ 0 & 7 & -11 \\ 0 & -3 & 8\end{array} \right].\end{displaymath}](img7.gif) |
(6) |
More details are found in
Claerbout and Muir (1973)
which is where I recovered this example.





Next: Curve through two points
Up: EXAMPLES
Previous: Best fitting straight line
Stanford Exploration Project
4/27/2000
![\begin{displaymath}
e_{ij} = \left[ \begin{array}
{rrr}
0& -12 & 4 \\ 17& 0 & 0 \\ 0& 10 & 0
\end{array} \right].\end{displaymath}](img2.gif)
![\begin{displaymath}
e_{ij} = \left[ \begin{array}
{rrr}
0& -12 & 4 \\ 17& 0 & 0 \\ 0& 10 & 0
\end{array} \right].\end{displaymath}](img2.gif)
![\begin{displaymath}
\left[ \begin{array}
{rrr}
0 & 0 & 16 \\ 5 & 0 & 0 \\ -12 & 10 & 0
\end{array} \right],\end{displaymath}](img4.gif)
![\begin{displaymath}
\left[ \begin{array}
{rrr}
0 & 0 & 4 \\ 5 & 0 & -12 \\ 0 & 22 & 0
\end{array} \right].\end{displaymath}](img5.gif)
![\begin{displaymath}
\left[ \begin{array}
{rrr}
0 & 0 & 0 \\ 0 & 7 & -11 \\ 0 & -3 & 8\end{array} \right].\end{displaymath}](img7.gif)