| (18) | ||
| (19) |
To minimize, simply cancel off u' and set to zero.
The thin plate equation resembles the biharmonic equation but differs in a subtle but important way. The quadratic form minimized for a thin plate is:
![\begin{displaymath}
T(u) \quad =\quad v'v
\quad
\quad
\quad
{\rm where \ }
v =
...
...{xy} \\ \partial_{yx} \\ \partial_{yy}
\end{array} \right] u\end{displaymath}](img23.gif) |
(20) |
| (21) |
Again, we find the associated differential equation by canceling off the u'.
What is bothering me is that the dispersion relations look the same but the quadratic forms look different. The difference between the biharmonic quadratic form and the thin plate quadratic form lies in the cross term. Let us form half this difference G=(B-T)/2.
| (22) |
By means of rotation of coordinates, we can diagonalize the matrix
| (23) |
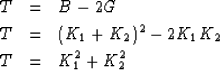 |
(24) | |
| (25) | ||
| (26) |
The meaning is this: The biharmonic equation zeroes B=(K1+K2)2 so its solution could be expected to have many places of K1=-K2 where the curvature on one axis is the negative of that on the other axis. In other words, solving the biharmonic equation might give us a function containing many saddles. On the other hand, the thin-plate equation T = K12 +K22 tries to eliminate both curvatures (not allowing credit for when one cancels the other). However, with respect to optimization, both quadratic forms are equivalent.