




Next: About this document ...
Up: Rickett: Traveltime sensitivity kernels
Previous: REFERENCES
Modeling with the first-order Born (and Rytov) approximations
[e.g. Beydoun and Tarantola (1988)] can be
justified by the assumption that slowness heterogeneity in the earth
exists on two separate scales: a smoothly-varying background,
s0, within which the ray-approximation is valid,
and weak higher-frequency perturbations, 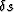 , that
act to scatter the wavefield.
The total slowness is given by the sum,
, that
act to scatter the wavefield.
The total slowness is given by the sum,
| 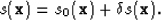 |
(10) |
Similarly, the total wavefield, U, can be considered
as the sum of a background wavefield, U0, and a
scattered field, 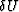 , so that
, so that
| 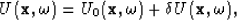 |
(11) |
where U0 satisfies the Helmholtz equation in the background
medium,
| ![\begin{displaymath}
\left[ \nabla^2 + \omega^2 \, s_0^2({\bf x})\right]
U_0({\bf x},\omega) = 0,\end{displaymath}](img31.gif) |
(12) |
and the scattered wavefield is given by the (exact) non-linear
integral equation Morse and Feshbach (1953),
| 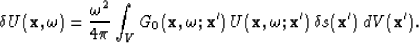 |
(13) |
In equation (13), G0 is the Green's function for
the Helmholtz equation in the background medium:
i.e. it is a solution of the equation
| ![\begin{displaymath}
\left[ \nabla^2 + \omega^2 \, s_0^2({\bf x})
\right] G_0({\bf x},\omega ; {\bf x}_s) = -4 \pi \delta({\bf x} -
{\bf x}_s). \end{displaymath}](img33.gif) |
(14) |
Since the background medium is smooth, in this paper I use Green's
functions of the form,
| 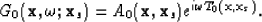 |
(15) |
where A0 and T0 are ray-traced traveltimes and amplitudes
respectively.
A Taylor series expansion of U about U0 for small 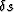 ,results in the infinite Born series, which is a Neumann series
solution Arfken (1985) to equation (13).
The first term in the expansion is given below: it corresponds
to the component of wavefield that interacts with scatters only once.
,results in the infinite Born series, which is a Neumann series
solution Arfken (1985) to equation (13).
The first term in the expansion is given below: it corresponds
to the component of wavefield that interacts with scatters only once.
| 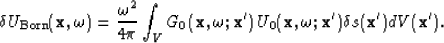 |
(16) |
The approximation implied by equation (16) is known as the
first-order Born approximation. It provides a linear relationship
between 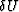 and
and 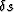 , and it can be computed more easily
than the full solution to equation (13).
, and it can be computed more easily
than the full solution to equation (13).
The Rytov formalism starts by assuming the heterogeneity perturbs the
phase of the scattered wavefield. The total field, 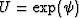 ,is therefore given by
,is therefore given by
| 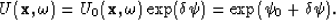 |
(17) |
The linearization based on small 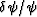 leads to the
infinite Rytov series, on which the first term is given by
leads to the
infinite Rytov series, on which the first term is given by
| 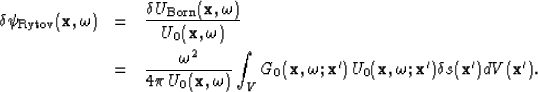 |
(18) |
| (19) |
The approximation implied by equation (19) is known as
the first-order Rytov approximation. It provides a linear relationship
between 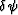 and
and 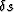 .
.





Next: About this document ...
Up: Rickett: Traveltime sensitivity kernels
Previous: REFERENCES
Stanford Exploration Project
4/27/2000
![]() , so that
, so that
![]() ,results in the infinite Born series, which is a Neumann series
solution Arfken (1985) to equation (13).
The first term in the expansion is given below: it corresponds
to the component of wavefield that interacts with scatters only once.
,results in the infinite Born series, which is a Neumann series
solution Arfken (1985) to equation (13).
The first term in the expansion is given below: it corresponds
to the component of wavefield that interacts with scatters only once.
![]() ,is therefore given by
,is therefore given by
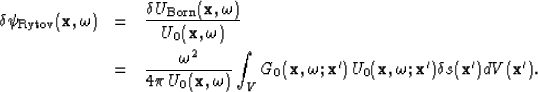
![]() and
and ![]() .
.