Another option is to characterize our model in terms of PEFs rather than steering filters. Normally we estimate a PEF by solving
| |
(3) |
| (4) | ||
|
patch
Figure 9 Non-stationary PEF construction. The model is broken up into micro-patches. Each micro-patch has its own PEF. | 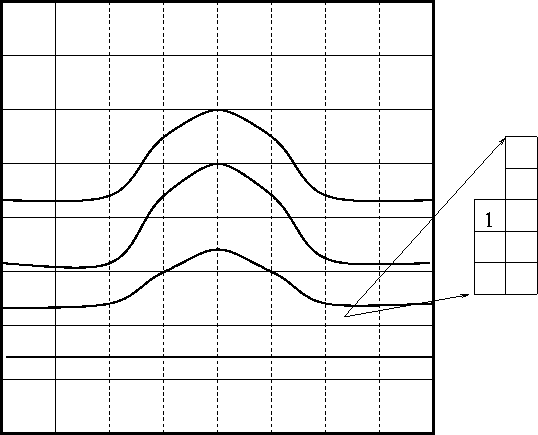 |