




Next: A quasi-Newton method for
Up: Definitions and Conditions for
Previous: Theorem
Let 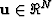 with
with 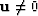 . For sufficiently small t we have
. For sufficiently small t we have
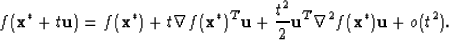
But 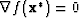 giving
giving
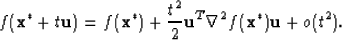
If 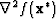 is positive definite, its smallest eigenvalue
is positive definite, its smallest eigenvalue 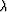 obeys
obeys 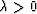 .So we have
.So we have
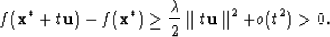
Then, 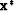 is a local minimizer for f.
is a local minimizer for f.
We see that a sufficient condition for a local minimizer is 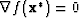 and
and
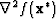 (Hessian) is positive definite.
These conditions are very important and should guide us in the choice of an optimization strategy.
(Hessian) is positive definite.
These conditions are very important and should guide us in the choice of an optimization strategy.
Quadratic functions form the basis for most of the algorithms in optimization, in particular
for the quasi-Newton method detailed in this paper. It is then important to discuss some issues
involved with these functions.
Now, if we pose a quadratic objective function
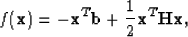
we see that we want to solve
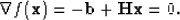
We may assume that the Hessian 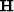 is symmetric because
is symmetric because
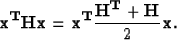
So, the unique global minimizer is the solution of the system above if 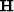 (the Hessian) is spd.
(the Hessian) is spd.





Next: A quasi-Newton method for
Up: Definitions and Conditions for
Previous: Theorem
Stanford Exploration Project
4/27/2000
![]()
![]()
![]()
![]() and
and
![]() (Hessian) is positive definite.
These conditions are very important and should guide us in the choice of an optimization strategy.
(Hessian) is positive definite.
These conditions are very important and should guide us in the choice of an optimization strategy.
![]()
![]()
![]()