




Next: Tests on synthetic data:
Up: comparing IRLS and Huber
Previous: comparing IRLS and Huber
Figure 2 shows the input data for the first synthetic example plus
the l2 inversion result; it demonstrates the sensitivity of least-squares to outliers:
some ellipses appear in the model space and
the data space is infested with noise. Figures 3 and
4 show a comparison
between IRLS and the Huber solver (same clip applied on the data).
The damping parameter for IRLS and the Huber threshold were chosen as suggested above
(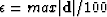 ).
Both results are very comparable since we get rid of the spikes in
the data space (Figure 3). In addition, the five expected
velocity events, associated with the five input hyperbolas, are clearly identifiable in the
model space (Figure 4).
Both results are very conclusive since the spikes have been correctly ``l1 handled''.
gr-spiky-L2-HUBER
).
Both results are very comparable since we get rid of the spikes in
the data space (Figure 3). In addition, the five expected
velocity events, associated with the five input hyperbolas, are clearly identifiable in the
model space (Figure 4).
Both results are very conclusive since the spikes have been correctly ``l1 handled''.
gr-spiky-L2-HUBER
Figure 2 From left to right: 1) Input data. 2) velocity
domain, l2 inversion result. 3) remodeled data from the l2 result




 comp-data-spiky-0.04
comp-data-spiky-0.04
Figure 3 From left to right: 1) Remodeled data with l2. 2)
Remodeled data with the Huber solver. 3) Remodeled data using IRLS




 comp-mod-spiky-0.04
comp-mod-spiky-0.04
Figure 4 From left to right: 1) l2 velocity space. 2) Huber
velocity space. 3) IRLS velocity space










Next: Tests on synthetic data:
Up: comparing IRLS and Huber
Previous: comparing IRLS and Huber
Stanford Exploration Project
4/27/2000



