




Next: comparing IRLS and Huber
Up: IRLS and the Huber
Previous: Minimizing the Huber function
The IRLS implementation of the hybrid l2-l1 norm differs greatly from the Huber solver.
In this section, I follow quite closely what Nichols (1994) and Darche (1989)
suggested in previous reports. The main idea is that instead of minimizing
the simple l2 norm, we can choose to minimize a weighted residual. The objective function becomes
| 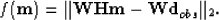 |
(4) |
A difference between the Huber solver and IRLS clearly arises here since we still
solve a least-square problem with IRLS and not with the Huber solver. The IRLS
method weights residuals within a linear l2 framework and Huber uses either
l2 or l1 following the residual with a nonlinear update.
A particular choice for 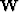 will lead to the minimization of the l2-l1 norm,
however. In this paper, I choose
will lead to the minimization of the l2-l1 norm,
however. In this paper, I choose
| ![\begin{eqnarray}
w_{ii}=\frac{1}{[1+(r_{ii}/\epsilon)^2]^{1/4}},\end{eqnarray}](img25.gif) |
(5) |
with 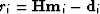 and
and  a damping parameter.
With this particular choice of W, minimizing f is equivalent to minimizing Bube and Langan (1997)
a damping parameter.
With this particular choice of W, minimizing f is equivalent to minimizing Bube and Langan (1997)
| 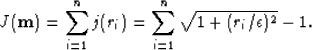 |
(6) |
For any given residual ri, we notice that
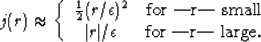
Hence, we obtain a l1 treatment of large residuals and a l2 treatment of small
residuals. Darche (1989) gives a practical value for  that can be also used for
the Huber threshold:
that can be also used for
the Huber threshold:
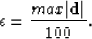
Two different IRLS algorithms are suggested in the literature Scales and Gersztenkorn (1988).
The first method consists of solving successive l2 problems with a constant weight and taking
the last solution obtained to recompute the weight for the next l2 problem. The second method
consists of recomputing the weights at each iteration (in fact, we need only a few iterations
of the conjugate gradient scheme before calculating the new weight), solving small piecewise linear
problems. The IRLS algorithms converge if each minimization reaches a minimum for a constant weight
Bube and Langan (1997). This is the case for the first method described above, but it is also true
for the second method since each starting point of the next iteration is the ending point
of the previous solving piecewise linear problems. For practical reasons, we utilize the second method.
Indeed, for most geophysical problems, the complete solution of the l2 problem with a constant
weight would lead to prohibitive costs. The general process in the program is as follows:
- 1.
- compute the current residual
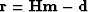
- 2.
- compute the weighting operator
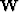 using
using 
- 3.
- solve the weighted least-squares problem (equation 4) using a Conjugate Gradient algorithm
- 4.
- go to first step
We do not detail the Conjugate Gradient step here. For more details, the reader may refer to
Paige and Saunders (1982). In our implementation, we control
the restarting schedule of the iterative scheme with one parameter that governs the periodic
computing of the weight. The Conjugate Gradient is reset for each new weighting function,
meaning that the first iteration of each new least-squares problem (for each new weight)
is a steepest descent step. In addition, the last solution 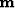 of the
previous least-squares problem is used to compute the new residual and the new
weighting matrix (steps 1 and 2 in the IRLS algorithm).
In the following examples, except when indicated, we recompute the weight every five iterations.
In the following sections, I call ``IRLS'' the IRLS algorithm described above with the weighting
function in equation (5).
of the
previous least-squares problem is used to compute the new residual and the new
weighting matrix (steps 1 and 2 in the IRLS algorithm).
In the following examples, except when indicated, we recompute the weight every five iterations.
In the following sections, I call ``IRLS'' the IRLS algorithm described above with the weighting
function in equation (5).





Next: comparing IRLS and Huber
Up: IRLS and the Huber
Previous: Minimizing the Huber function
Stanford Exploration Project
4/27/2000
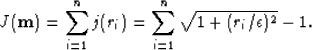
![]()
![]()