




Next: IRLS and the Huber
Up: Guitton: IRLS vs. Huber
Previous: Guitton: IRLS vs. Huber
Robust error measures such as the l1 norm have a number of
uses in geophysics. As measures of data misfit, they show considerably
less sensitivity to large measurement errors than does the least-squares
(l2) measure. In a recent work, Guitton and Symes (1999) show that a possible
approximation of the l1 norm is viable using the Huber misfit function Huber (1973).
In particular, their work on velocity inversion, using the hyperbolic
Radon transform, suggests that (1) the Huber function gives far more robust
model estimates than does least squares, (2) its minimization using a standard
quasi-Newton method is comparable in computational cost to least-squares estimation
using conjugate gradient iteration, and (3) the result of Huber data fitting is stable
over a wide range of choices for the 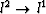 threshold and total number of
quasi-Newton steps. For the same geophysical problem, Nichols (1994) and Hugonnet (1998)
use a different implementation of the hybrid l2-l1 norm, using an IRLS
algorithm with a thoroughly chosen weighting function.
Both strategies (IRLS and the Huber solver) show similar results, but at this stage,
no direct comparisons between the two methods have been carried out.
threshold and total number of
quasi-Newton steps. For the same geophysical problem, Nichols (1994) and Hugonnet (1998)
use a different implementation of the hybrid l2-l1 norm, using an IRLS
algorithm with a thoroughly chosen weighting function.
Both strategies (IRLS and the Huber solver) show similar results, but at this stage,
no direct comparisons between the two methods have been carried out.
This paper will compare the efficiency of the these two robust solvers with synthetic and real data.
First, I will briefly review both methods and describe
algorithmic issues. Then, I will compare the Huber solver and IRLS performing velocity inversion
as suggested by Thorson and Claerbout (1985), Nichols (1994), and Lumley et al. (1994).





Next: IRLS and the Huber
Up: Guitton: IRLS vs. Huber
Previous: Guitton: IRLS vs. Huber
Stanford Exploration Project
4/27/2000