 |
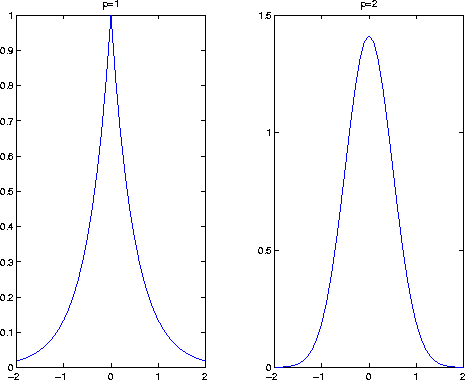
Figure 1 Exponential (left) and Gaussian (right) distribution with zero mean. The exponential distribution has the longer tail.
Some authors have proposed different solutions to address the sparseness of the model space. Thorson and Claerbout (1985) developed a stochastic inversion scheme that converges to a solution with minimum entropy. Sacchi and Ulrych (1995) apply a very similar method with more degrees of freedom to the choice of parameters. Nichols (1994) uses a regularization term with the l1 norm. All these methods assign long-tailed density functions to the model parameters. Figure 1 shows an exponential (related to the l1 norm) and a Gaussian distribution (related to the l2 norm). The Gaussian distribution will tend to smooth the model space, spreading the energy, whereas the exponential distribution will tend to focus the energy on a few peaks, neglecting average values, and thus leading to a sparse model.
 |