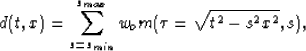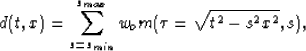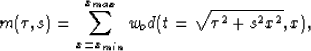Next: The inverse problem
Up: THEORY
Previous: THEORY
The HRT maps the data (t, x) into a velocity space
( ,v) that clearly exhibits the moveout inherent in the
data and, therefore, forms a convenient basis for velocity analysis.
Thorson and Claerbout (1985) were the first to define the forward and adjoint operators
of the HRT, formulating it as an inverse problem, where the velocity domain
is the unknown space. In their approach, the forward operator H stretches the model
space (velocity domain) into the data space (CMP gathers) using a hyperbola
superposition principle, whereas the adjoint operator
,v) that clearly exhibits the moveout inherent in the
data and, therefore, forms a convenient basis for velocity analysis.
Thorson and Claerbout (1985) were the first to define the forward and adjoint operators
of the HRT, formulating it as an inverse problem, where the velocity domain
is the unknown space. In their approach, the forward operator H stretches the model
space (velocity domain) into the data space (CMP gathers) using a hyperbola
superposition principle, whereas the adjoint operator 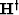 , the HRT,
squeezes the data summing over hyperbolas (related to the velocity stack as defined by
Taner and Koehler (1969)). The forward operation is
, the HRT,
squeezes the data summing over hyperbolas (related to the velocity stack as defined by
Taner and Koehler (1969)). The forward operation is
| 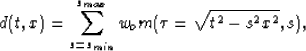 |
(1) |
and the adjoint transformation becomes
| 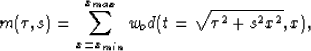 |
(2) |
where x is the offset, s the slowness,  the two-times zero offset
travel time, and wo a weighting function that compensates to
some extent for geometrical spreading and other effects Claerbout and Black (1997).
the two-times zero offset
travel time, and wo a weighting function that compensates to
some extent for geometrical spreading and other effects Claerbout and Black (1997).





Next: The inverse problem
Up: THEORY
Previous: THEORY
Stanford Exploration Project
4/27/2000