Next: Application to Kirchhoff imaging
Up: Clapp et al.: Kirchhoff
Previous: Introduction
Model resolution operator 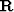 defines the connection between
the true model
defines the connection between
the true model 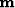 and the model estimate from least-squares
inversion
and the model estimate from least-squares
inversion 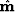 , as follows:
, as follows:
| 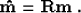 |
(1) |
In the case of least-squares Kirchhoff migration, 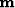 corresponds to true reflectivity,
corresponds to true reflectivity, 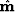 is the output
image, and the estimation process amounts to minimizing the least-square
norm of the residual
is the output
image, and the estimation process amounts to minimizing the least-square
norm of the residual 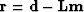 , where
, where 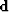 is
the observed data, and
is
the observed data, and 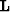 is the Kirchhoff modeling operator.
Recalling the well-known formula
is the Kirchhoff modeling operator.
Recalling the well-known formula
| 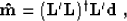 |
(2) |
where 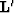 stands for the adjoint operator (Kirchhoff
migration), and the dagger symbol denotes the pseudo-inverse operator,
we can deduce from formulas (3) and (2) that
stands for the adjoint operator (Kirchhoff
migration), and the dagger symbol denotes the pseudo-inverse operator,
we can deduce from formulas (3) and (2) that
| 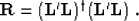 |
(3) |
In
the ideal case, when all model components are perfectly resolved,
the model resolution model matrix is equal to the identity. If the model
is not perfectly constrained, the inverted 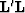 matrix will
be singular, and the model resolution will depart from being the
identity. It means that the model contains some null-space components
that are not constrained by the data. The diagonal elements of the
resolution matrix will be less than one in the places of unresolved
model components.
matrix will
be singular, and the model resolution will depart from being the
identity. It means that the model contains some null-space components
that are not constrained by the data. The diagonal elements of the
resolution matrix will be less than one in the places of unresolved
model components.
Berryman and Fomel (1996) derive the following remarkably simple formula
for the model resolution matrix:
| 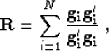 |
(4) |
where N corresponds to the model size, and the 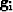 's are the
model-space gradient vectors that appear in the conjugate-gradient
process Hestenes and Stiefel (1952). In large-scale problems, such as a typical
Kirchhoff migration, we cannot afford performing all N steps of the
conjugate-gradient process, required for the theoretical convergence
of the model estimate to the one defined in formula (2).
However, formula (4) is still valid in this case, if we
replace number N with the actual number of steps. In this case, the
matrix R corresponds to the actual resolution of our estimate. To
reduce the computational effort, we can use formula (4)
only with a few significant gradient vectors
's are the
model-space gradient vectors that appear in the conjugate-gradient
process Hestenes and Stiefel (1952). In large-scale problems, such as a typical
Kirchhoff migration, we cannot afford performing all N steps of the
conjugate-gradient process, required for the theoretical convergence
of the model estimate to the one defined in formula (2).
However, formula (4) is still valid in this case, if we
replace number N with the actual number of steps. In this case, the
matrix R corresponds to the actual resolution of our estimate. To
reduce the computational effort, we can use formula (4)
only with a few significant gradient vectors 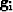 to obtain an
effective approximation of the model resolution. The most significant
to obtain an
effective approximation of the model resolution. The most significant
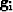 's will turn out to be those have large components in the
direction of eigenvectors having large eigenvalues (or singular vectors
have large singular values).
's will turn out to be those have large components in the
direction of eigenvectors having large eigenvalues (or singular vectors
have large singular values).
The next section exemplifies this approach with synthetic and real
data tests.





Next: Application to Kirchhoff imaging
Up: Clapp et al.: Kirchhoff
Previous: Introduction
Stanford Exploration Project
10/25/1999
![]() defines the connection between
the true model
defines the connection between
the true model ![]() and the model estimate from least-squares
inversion
and the model estimate from least-squares
inversion ![]() , as follows:
, as follows:
![]() matrix will
be singular, and the model resolution will depart from being the
identity. It means that the model contains some null-space components
that are not constrained by the data. The diagonal elements of the
resolution matrix will be less than one in the places of unresolved
model components.
matrix will
be singular, and the model resolution will depart from being the
identity. It means that the model contains some null-space components
that are not constrained by the data. The diagonal elements of the
resolution matrix will be less than one in the places of unresolved
model components.